¿Cuánto mide la cuerda?

Aún estamos con la resaca de Cheryl y su problema (bueno, en realidad el problema era para los participantes de las últimas SASMO, Singapore and Asian Schools Math Olympiads) y ya está empezando a correr por las redes otro problema, aunque este tiene bastante más tiempo que el de Cheryl.

Hace 20 años la Asociación Internacional para la Evaluación de Logros Académicos (IEA), propuso tres problemas a estudiantes de secundaria de matemáticas avanzadas de 16 países de todo el mundo. El que vamos a ver es uno de esos tres problemas. Y preguntaréis ¿por qué vamos a ver ese en concreto? Pues porque resulta que sólo supo resolverlo el 10% de los estudiantes (el 4% en Estados Unidos y el 24% en Suecia).

La asociación explicó que este problema fue el que más gente falló, y no porque sea especialmente difícil de resolver, todo lo contrario. De hecho a penas se resuelve en dos líneas y con algo muy familiar para todas y todos (que hayan recibido una enseñanza matemática por supuesto, pero básica).

Yo no lo compararía con el problema de lógica del cumpleaños de Cheryl que, si bien es cierto que tienen en común que no hace falta saber muchas matemáticas para resolverlos, éste se basa más bien en tener lo que se suele llamar una “idea feliz”.

El enunciado del problema es el siguiente:

“Una cuerda está enrollada de forma simétrica alrededor de una barra circular. La cuerda da la vuelta exactamente cuatro veces alrededor de la barra, que tiene una circunferencia de 4 centímetros y una longitud de 12 centímetros. Averigua cuánto mide la cuerda”.

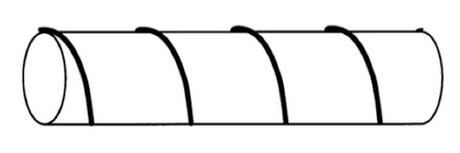
Tomaros el tiempo que necesitéis para resolverlo.

¿Lo tenéis ya?

Bueno, si no es así no hay problema, vamos a ver como podemos resolverlo.

Si no quieres ver la SOLUCIÓN aún…. ¡no sigas bajando!

Así a primera vista se antoja algo complicado obtener la longitud de la cuerda tal y como está, dando vueltas alrededor de un cilindro. Pero aquí es donde viene la “idea feliz”.

El problema se vuelve mucho más sencillo si pensamos en la barra como en una superficie plana.

Es como si tuviéramos el cartón con forma de cilindro en el que está enrollado el papel del baño (el cartón de dentro de un “rollo de papel higiénico”, así se dice en España) y lo cortásemos longitudinalmente. Al abrirlo nos quedaría un rectángulo.

En nuestro caso nos quedaría así:

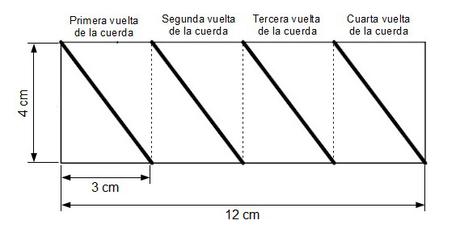
¡Mucho mejor ahora!

Si nos fijamos en la parte inferior de la izquierda, podemos ver que se ha formado un triángulo rectángulo.

Y, una vez más, como ocurría con el problema del televisor y con otros tantos problemas, nuestro gran salvador es… ¡El Teorema de Pitágoras!

Recordemos lo que decía el Teorema de Pitágoras: “en todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”

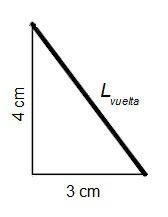
Sabemos que uno de los catetos mide 4 centímetros y el otro 3 centímetros (es una cuarta parte de la longitud total de la barra, 12 cm). La hipotenusa es la longitud de una vuelta de la cuerda.

Así que, aplicando el Teorema de Pitágoras podemos calcular la hipotenusa, es decir, la longitud de una vuelta de la cuerda.

(Observad, que de las dos soluciones, positiva y negativa, que tiene la ecuación cuadrática anterior (ecuación de segundo grado), tan solo he considerado al final la positiva (5 cm), porque como se trata de una longitud, no tiene sentido la solución negativa.)

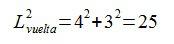
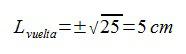
Sabiendo ya la longitud de la cuerda en una vuelta, podemos calcular la longitud total de la cuerda simplemente multiplicando por 4, ya que son cuatro vueltas las que da la cuerda alrededor de la barra.

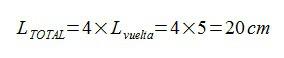
Viéndolo así no parece nada complicado ¿verdad? Cabe preguntarse por qué fueron tan malos los resultados en la prueba con este problema. Lo cierto es que, por desgracia, se les enseña a los alumnos y alumnas conceptos, fórmulas y procedimientos de cálculo… pero no a que aprendan a pensar de forma creativa y a que utilicen su imaginación, y las matemáticas tienen mucho más de esto último que de lo anterior.