El acertijo propuesto es el siguiente:
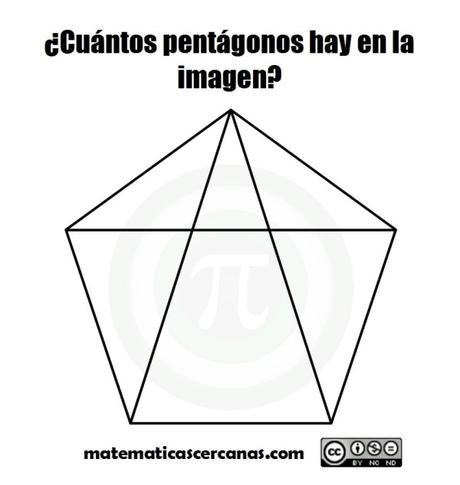
Se trata, por tanto, de encontrar el mayor número posible de pentágonos siguiendo las líneas de la imagen.
Indicar también que no se trata de una vista de una figura tridimensional (hubiese quedado mal definida si hubiese sido así al faltar información de otras vistas de la misma), sino de una composición de líneas en el plano.
Si aún no lo habías visto o simplemente no lo has intentado resolver todavía, te invito a que lo hagas primero antes de seguir leyendo esta entrada.
Si quieres saber ya la solución…
¡Vamos con ella!
Empezaré definiendo qué es un pentágono, y así nos basaremos en su propia definición para buscarlos:
“Un pentágono es un polígono de cinco lados y cinco vértices”
Pues busquemos polígonos de cinco lados y cinco vértices.
Seguramente, lo primero que todo el mundo ha visto es el pentágono regular exterior…
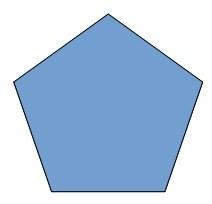
Que sea regular quiere decir que sus cinco lados y sus cinco ángulos son iguales, o mejor dicho, congruentes entre sí.
Aunque nada en la figura (acotación) indica que tenga por qué ser regular, como he dicho con total seguridad todo el mundo lo habrá identificado como tal (de hecho lo es y basta con tomar medidas de sus lados o de sus ángulos para comprobarlo).
Es más, para muchos es el único pentágono en este acertijo. Y la culpa de que esto ocurra es más de que casi siempre nos “venden” así los pentágonos y, en consecuencia es la imagen “exclusiva” que muchas personas tienen de ellos (basta con mirar las imágenes de pentágonos de los libros de texto o incluso de la famosa Wikipedia).
Pero también hay pentágonos irregulares, en los que no todos los lados ni todos los ángulos son iguales.
Simplemente se nos pregunta por pentágonos, en ningún sitio digo que tengan que ser regulares, así que sigamos identificando polígonos de cinco lados…
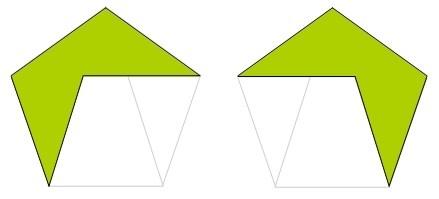
… muy parecidos a éstos tenemos…
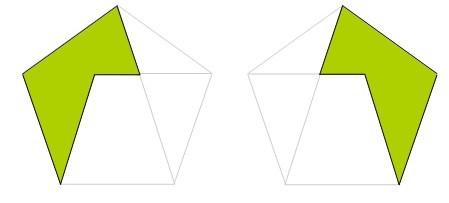
… y aún podemos encontrar más…

… y estos otros dos también…
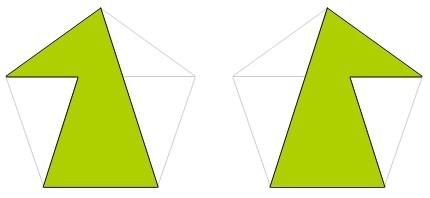
Si hacemos recuento, hemos encontrado 9 pentágonos (1 pentágono regular y 8 irregulares).
A esta respuesta han conseguido llegar algunas personas. Otras, la mayoría, se han quedado en el camino y han dado como solución un número intermedio entre 1 y 9.
No obstante, lo importante es que tenían claro que los pentágonos no tenían por qué ser solo regulares, pudiendo ser también irregulares, y simplemente no han llegado a ver alguno de ellos (es fácil que se nos escapen algunos si no lo revisamos unas cuantas veces, la verdad).
Bien, pero…
¿Aquí acaba todo esto?
Si eres observador habrás visto que en la segunda imagen de esta entrada, en la que preguntaba “¿Quieres ver la solución?”, decía justo antes “No son 1, ni 2, ni 3… ni 8, ni 9… son más“.
Efectivamente hay más pentágonos.
Hasta ahora todos los pentágonos que hemos identificado, regulares e irregulares, eran polígonos simples.
Quizás te preguntes…
¿Qué es eso de polígonos simples?
Y pensarás que simple, lo que se dice simple (pensando en simple como “sencillo”), lo era desde luego el primero.
Cuando hablo de polígonos simples me refiero a aquellos en los que ningún par de lados no consecutivos se corta.
Y fíjate que he dicho “no consecutivos“, ya que los lados consecutivos se cortan en los vértices.
Y esto último que he dicho es muy importante pues, si lo leemos al revés, nos da la definición de vértice como el punto de intersección de dos lados consecutivos.
Y eso es lo que pasaba en todos los pentágonos que hemos visto hasta ahora, solo se cortaban los lados consecutivos y lo hacían en los vértices.
Pero puede ocurrir que uno o más pares de lados no consecutivos se corten, y en ese caso lo que tenemos son polígonos complejos.
De hecho, si lo piensas, lo más normal en esta vida es que las cosas sean complejas y no simples (esto ya no es matemático, es una reflexión mía).
¿No lo terminas de ver?
No te preocupes, que te voy a enseñar uno de los que podemos encontrar…
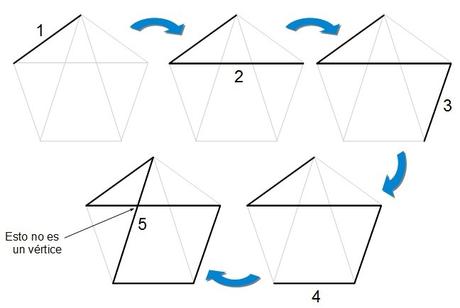
Como se indica en la última figura, el punto donde se cortan los lados 2 y 5 no es un vértice, pues por definición hemos dicho que un vértice es el punto de intersección de dos lados consecutivos, y éstos no lo son.
Así que tenemos este pentágono que hemos visto y el que obtenemos por simetría de la figura…
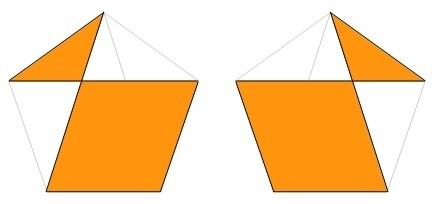
Y hay otros dos más muy parecidos…
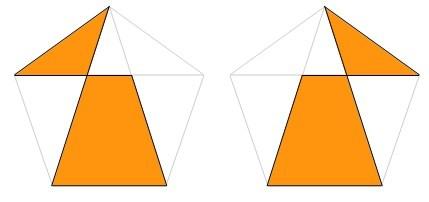
¿Cuántos llevamos ya?
Hagamos de nuevo recuento…
9 pentágonos simples (1 regular y 8 irregulares) más 4 pentágonos complejos…
¡13 pentágonos!
¿Habrá alguno más?
Si me conoces un poco ya, sabrás que la respuesta es sí. Nos queda este otro…
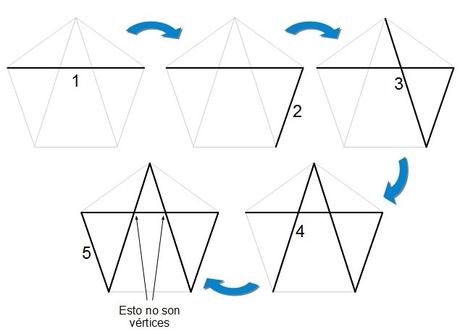

Y ya sí que no hay más.
No está nada mal, en una figura tan sencilla hemos encontrado 14 pentágonos.
Y esa es la solución de este acertijo que os he propuesto y que, además de haberos entretenido, espero que haya servido para aprender algo más de los distintos tipos de polígonos.
Por cierto que este acertijo tiene un hermano mayor que propuse hace ya un año y medio y que sí que es un verdadero reto…

¿Te atreves?
Te diré que hay nada más y nada menos que… ¡132 hexágonos!
Si quieres ver la resolución detallada la tienes aquí:
SOLUCIÓN ¿Cuántos hexágonos hay dibujados en la imagen?
Como siempre, muchas gracias por estar ahí.
¡Ah!
Una última cosa…
Este post forma parte del Carnaval de Matemáticas, que en esta septuagésima segunda edición, también denominada 8.2, está organizado por Rafael Martínez González a través de su blog El mundo de Rafalillo.
Os recomiendo visitar las entradas participantes porque seguro que os gustarán.
¡Qué se me olvida!
Enhorabuena a mi amiga Ada que ha sido la única persona (al menos hasta donde yo he podido observar) que, entre cientos de respuestas que ha habido en las redes sociales a este acertijo de los pentágonos, ha dado la solución correcta.
Aunque no signifique mucho, porque lo que yo hago aquí apenas supone nada, quiero dedicarle esta entrada a mi cuñado Alberto, que siempre ha mostrado interés por los acertijos que propongo, y que lo está pasando realmente mal. Utilizando la terminología de esta entrada, para muchas personas, como su hermano Dani y mi hermana, la vida no ha sido nada simple y al final ha resultado demasiado compleja, tanto que no les ha permitido ser ellas mismas y poder seguir con nosotros.

