Claro está, el vídeo tiene connotaciones matemáticas que como habrás adivinado hacen referencia a la triangulación. Éste es un concepto amplio, que hace referencia a:
- El cálculo de distancias y ángulos (problemas trigonométricos) que permiten localizar distancias entre puntos/lugares innacesibles o puntos/lugares a mucha distancia entre ellos, Willebrord Snell, en 1615 estudió la distancia de Alkmaar a Bergen-op-Zoom, aproximadamente 70 millas (110 kilómetros), utilizando un conjunto de 33 triángulos
- La localización de puntos en el plano (propiedad usada hoy en día GPS)
- Y al cálculo de áreas de polígonos irregulares.
Los métodos de triangulación tienen sus orígenes en el Antiguo Egipto y en la necesidad de delimitar el terreno perteneciente a cada uno después de la inundaciones anuales del Nilo.
El modo de calcular el área de un polígono irregular como la suma de las áreas de los triángulos, es un método que fue propuesto por primera vez por el sabio griego Antifón hacia el año 430 a. C.y tiene la ventaja de que solo necesitamos saber la fórmula del área del triángulo para calcular el área de cualquier polígono irregular.
Por ejemplo, el siguiente polígono irregular de siete lados (heptágono) está dividido en cinco triángulos:
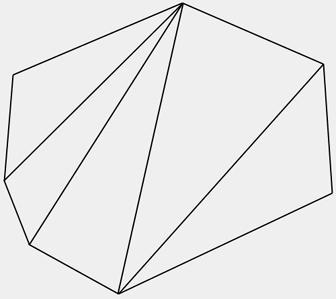
Para calcular el área de cada uno de los triángulos se propone usar la fórmula de Herón, geómetra griego del siglo I de nuestra era, en el cual únicamente se requieren las medidas de los tres lados del triángulo y no la altura como en la fórmula clásica. La fórmula de Herón hace uso de un valor parcial, el semiperímetro (p), para después usarlo en la fórmula del área:
p = (a+b+c)/2
a = Raiz Cuadrada (p·(p-a)·(p-b)·(p-c))
Como veis, comenzamos por un vídeo realizado en la actualidad y hemos terminado con Herón en el siglo I D.C., un largo recorrido pero que por supuesto merece la pena.
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure