De Tales a Pitágoras en la esquina de una página

Hace un tiempo era normal marcar los puntos de lectura en un libro (por donde hemos dejado de leer para continuar en otro momento) doblando la esquina superior o inferior de la página.

Pero, alguien pensará que esto es todo un atentado a la integridad del libro…

… Y no le faltará razón, pues aunque intentemos “deshacer el mal”, la marca se queda ya en la página… y desde pequeños nos han dicho siempre que los libros hay que cuidarlos (gran verdad).

Además, para esto están precisamente los marcapáginas que, si tenemos niños en las primeras etapas escolares desplegando su creatividad en forma de manualidades, no nos faltarán, a no ser que hayan desaparecido “misteriosamente” (sí, esos duendes que entran por la noche en casa cuando estamos todos dormidos y se llevan algunos de los dibujos y manualidades fruto de la incesante y prolífera creatividad de nuestros hijos… ¡Qué insensibles!).

Pero volvamos a la doblez de la esquina de la página porque, a pesar de suponer un acto un tanto irresponsable, podemos aprender matemáticas con ella.

¿Matemáticas con una esquina doblada?

Sí, de hecho vamos a demostrar con ella el Teorema de Pitágoras.

 Manos a la obra…

Lo primero es, una vez que tenemos hecho el pliegue, unir el vértice de la esquina doblada de la página con el vértice de la página que se ve detrás.

Como no quiero continuar “atentando” contra el libro, me váis a permitir que lo represente virtualmente…

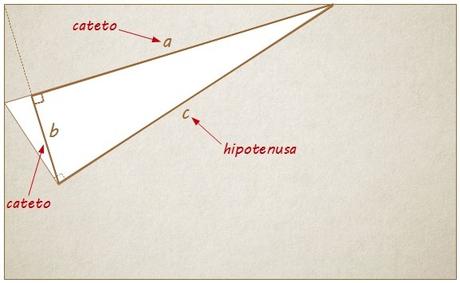
De esta manera se crean los siguientes tres triángulos rectángulos:

T(a,b,c)…

T(b,e,d)…

y T(c,d,a+e)…

Pues bien, vamos a fijarnos ahora en cómo son los lados de cada uno de estos triángulos respecto de los de los otros triángulos.

Por ejemplo, consideremos los triángulos T(a,b,c) y T(b,e,d), y llamemos a los ángulos del primero α (alpha) y β (beta). El tercer ángulo, al ser un triángulo rectángulo, está claro que es un ángulo recto (de 90 grados).

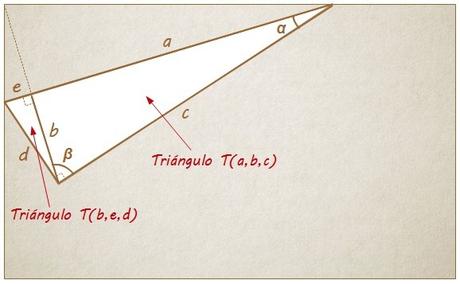
Si nos fijamos, los lados a y c de T(a,b,c) son perpendiculares a los lados b y d de T(b,e,d) respectivamente y, en consecuencia, ambas parejas de lados forman el mismo ángulo cada una (que hemos llamado α)…

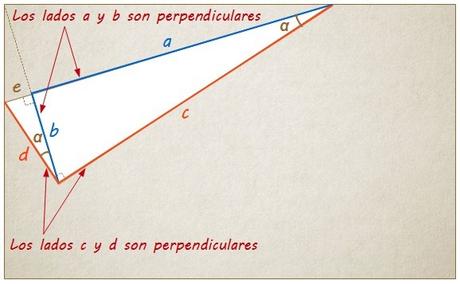
Lo mismo ocurre con los lados b y c de T(a,b,c), que son perpendiculares a los lados e y d de T(b,e,d) respectivamente, formando ambas parejas de lados el mismo ángulo, que en este caso hemos llamado β…

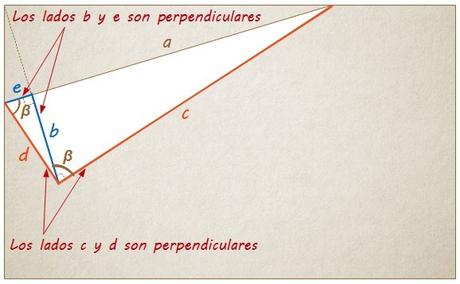
El tercer ángulo que tienen ambos triángulos rectángulos en común es, precisamente, el ángulo recto (el de 90 grados).

Dos triángulos que tienen sus ángulos homólogos iguales se dice que son semejantes (digamos que tienen la misma forma pero distinto tamaño) y, como hemos visto que T(a,b,c) y T(b,e,d) los tienen son, por tanto, semejantes.

¿Sucede lo mismo con los triángulos T(a,b,c) y T(c,d,a+e)?

Viendo las imágenes de cada uno con los ángulos que conocemos ya representados, está claro que también son semejantes, pues sus ángulos homólogos son iguales.

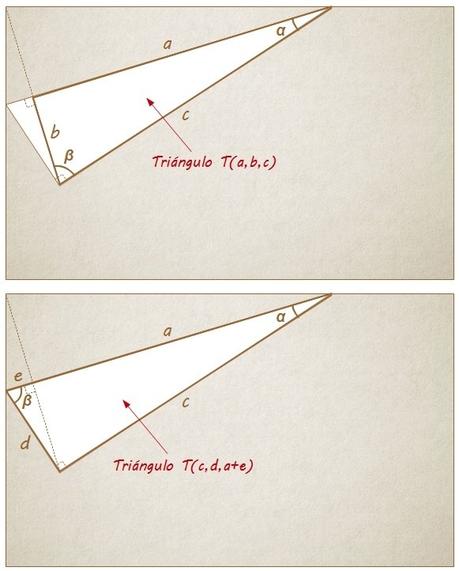
Y lo mismo ocurre con la otra pareja de triángulos que nos queda, T(b,e,d) y T(c,d,a+e).

Es decir, los tres triángulos son semejantes.

Que sean semejantes implica que, según el Teorema de Tales, sus lados homólogos son proporcionales.

Aplicando esto a nuestros tres triángulos tenemos…

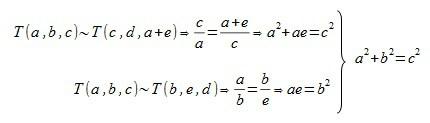
Con lo cual acabamos de demostrar que en el triángulo rectángulo creado por el pliegue de la esquina de la página y nuestra línea “virtual” se cumple que el cuadrado de la hipotenusa (c) es igual a la suma de los cuadrados de los catetos (a y b), que es lo que dice el Teorema de Pitágoras.

Y, lógicamente, puesto que son semejantes, también se cumple en el propio triángulo rectángulo que se forma con el pliegue.

Esta entrada participa en la Edición 7.6 “La banda de Möbius” del Carnaval de Matemáticas que, en esta ocasión, organiza Gaussianos.