En 1907, el creador de puzles Henry Dudeney publicó un acertijo que se convirtió en un quebradero de cabeza para los matemáticos del siglo XX. Hubo que esperar cien años, hasta 2007, para que un estudiante del MIT consiguiera resolverlo. ¿Es fácil entender la solución de un problema así?
Todo esto se basa en e l muestra que teorema de Wallace-Bolyai-Gerwien dos polígonos con igual área que admiten una disección en un número finito de piezas, donde uno puede girar de manera arbitraria y traducir las piezas para ir de un polígono a otro.
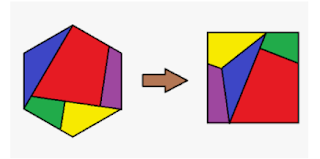
Existe un antiguo acertijo "El acertijo del mercero" ( "The Haberdasher's Puzzle") como problema número 26 en la recopilación "Los acertijos de Canterbury" ( "The Canterbury Puzzles"), libro publicado por H.E. Dudeney en 1907, que narra la historia de un grupo de peregrinos con destino al santuario de San Thomas Becket en Canterbury. Los peregrinos se proponen uno a otros rompecabezas para entretenerse durante el camino.
"Dudeney construyó la solución al acertijo en madera de ébano uniendo las cuatro piezas con bisagras de forma que al girar las piezas con un movimiento de la mano se podía pasar de una figura a la otra. Debido a ello se denomina como al tipo especial de "disección de Dudeney"disección de figuras geométricas en la que todas las piezas están conectadas en una cadena por puntos "bisagra", de tal manera que la transformación de una figura a otra puede llevarse a cabo haciendo pivotar la cadena de forma continua, sin cortar ninguna de las conexiones. En inglés de denominan también "higed dissections" (hinge puede ser traducido como bisagra, gozne o articulación que gira) El mercero se resistía a satisfacer las demandas de los peregrinos para que propusiera un acertijo. Tanto le insistieron... que al final se decidió, pidiendo que se le diera un paño en el que recortó un triángulo equilátero perfecto. Luego, mostrándolo a los demás dijo: "¿Es alguno de vosotros tan diestro en el corte de género como yo? Estimo que no. Cada hombre a su oficio, aunque el estudioso puede aprender del lacayo y el sabio del necio. Mostradme, pues, una manera de cortar este trozo de género en cuatro piezas de manera que puedan reunirse formando un cuadrado perfecto". Tras varios intentos, los más avezados mostraban soluciones cortando en triángulo en ¡cinco piezas! .... pero no en las cuatro que pedía el mercero. Mientras, él los observaba pero permanecía en silencio. Cuando finalmente le pidieron la solución casi recibe una paliza, pues, declaró que la había olvidado. Al fin, tras varias noches de incertidumbre, el acertijo quedó resuelto". Disecciones 2-DExisten varios tipos de disecciones.
Dos figuras se dicen equicompuestas si cortando de cierto modo una de ellas en un número finito de partes, se puede, al disponer estas partes de otra forma, componer con ellas la segunda figura. Claramente, si dos figuras son equicompuestas tienen la misma área. La pregunta recíproca de si dos figuras con la misma área son equicompuestas no tiene una respuesta tan evidente.
El teorema de Wallace-Bolyai-Gerwien establece que tiene una respuesta afirmativa en el caso de los polígonos: Si dos polígonos tienen igual área uno de ellos se puede dividir en partes de forma que es posible componer el segundo trasladando y rotando las piezas obtenidas en la disección. Polígono quiere decir, en este contexto, una figura limitada por un número finito de líneas quebradas formadas por un número finito de segmentos rectilíneos. Puede tener "agujeros". Lo importante es que sea posible dividir la figura en un número finito de triángulos.
Si damos el salto de dimensión 2 a dimensión 3 nos preguntaremos si con los poliedros pasa algo análogo. Dos poliedros se dicen equicompuestos si al cortar de cierto modo uno de ellos en un número finito de piezas poliédricas, se puede, al disponer estas piezas de otra forma, componer con ellas el segundo. De forma semejante al caso de los polígonos, claramente, si dos poliedros son equicompuestos tiene el mismo volumen. En este caso la pregunta recíproca de si dos poliedros con el mismo volumen son siempre equicompuestos tiene respuesta negativa.
Se trata de un problema difícil; el tercero en la famosa colección de 23 problemas compilados por Hilbert para la conferencia en París del Congreso Internacional de Matemáticos de 1900 con el objeto de estimular la investigación matemática durante el nuevo siglo. El propio Hilbert, basándose en trabajos de Gauss, ya conjeturó la imposibilidad de equicomponer algunos poliedros del mismo volumen. Y en el mismo año 1900, el matemático Max Wilhelm Dehn, nacido en Alemania y alumno de Hilbert, demostró como contraejemplo que el cubo y el tetraedro del mismo volumen no son equicompuestos.
Según el teorema de Dehn en el caso de los poliedros no es equivalente equicomposición y tener el mismo volumen.
Fuera del espacio de Euclides
Si abandonamos el mundo euclídeo tenemos que, tanto en la geometría hiperbólica como en la esférica, en dos dimensiones para los polígonos sigue siendo equivalente tener la misma área y ser equicompuestos. Pero en ambas geometrías sigue siendo desconocido que sucede en tres dimensiones; no se sabe si para los poliedros es equivalente o no, tener el mismo volumen y ser equicompuestos.
Rompecabezas de otro tipo
Basándose en las propuestas de Dudeney, se han construido casas de geometría variable.
Esta casa "ecológica, versátil y adaptable" está diseñada para cambiar según las condiciones ambientales. Los gruesos muros externos y las pequeñas ventanas se convierten en paredes internas, a la vez que las paredes interiores de vidrio pasan a ser las fachadas. Las puertas se convierten en ventanas y viceversa. Según sus diseñadores "para la época de invierno, la casa en forma cuadrada, con pequeñas ventanas y gruesas paredes, se abraza a sí misma. Para tiempo más cálido, la casa se abre como una flor para permitir que la luz y el aire penetren en el interior del edificio y ofrecer completas vistas panorámicas de los alrededores".
El descubrimiemto de Dudeney, aún no completamente desarrollado, ha abierto el camino a atrevidos diseños de ingeniería y arquitectura que veremos en próximos años.
----
https://es.qwe.wiki/wiki/Hinged_dissection
https://www.gutenberg.org/files/27635/27635-h/27635-h.htmAcertijos históricos:
Demo en Geogebra
https://images.math.cnrs.fr/La-cuadratura-del-triangulo.html?lang=fr http://sunya00.blogspot.com/2016/01/una-casa-con-geometria-dinamica.html https://www.geogebra.org/m/gwJ8g6cw http://www2.caminos.upm.es/Departamentos/matematicas/revistapm/revista_impresa/numero_2/juegos_dudeney.pdf