Dos formas de sumar

Hoy voy a cambiar un poco la temática del blog. Voy a hablar de Matemáticas. Dado que de vez en cuando escribo en el blog de Mati -en nombre de Mr. Green-, hoy lo haré en el mío tratando las Matemáticas, porque las Matemáticas no sólo son una ciencia, sino que es una disciplina que te ayuda a pensar más claramente y, por lo tanto, todo el mundo debería conocer al menos en sus niveles más básicos.
Hoy he leído en la página de Europa Press una noticia sobre una adolescente, Marta Espejel, de primero de Bachillerato que ha logrado simplificar la suma de los 100 primeros números naturales. En esta noticia enlazan con el blog del instituto donde estudia Marta y allí se detalla cómo lo hizo.
Después, resumiré otro modo de sumar los 100 primeros números, aplicable a los 100, 1000 o 10000 primeros y que puede calcularse mentalmente.
Divide y vencerás
En primer lugar, Marta sumó hasta los 16 primeros términos: sumó los dos primeros, los tres primeros, los cuatro primeros, etc. hasta llegar a la suma de los 16 primeros términos.
Pizarra de Marta. Créditos: IES Profesor Máximo Trueba / M. Espejel.
Posteriormente agrupó los resultados de dos en dos y observó que éstos eran múltiplos de 2, 3, 4, etc. y vio que cada uno de estos se descomponían también en el producto de dos factores.
Además, las sumas con un número impar de términos, uno de esos factores coincidía con el número de términos (Así, en el resultado de la suma de los 13 primeros términos, un factor es el número 13.
El otro factor se obtenía dividiendo entre 2 la suma del número de términos más 1. Por ejemplo, en la serie del 13 términos, el otro factor sería (13+1)/2=7.
Entonces, para hallar la suma de los 99 primeros números, un factor de esa suma sería 99 y el otro, (99+1)/2=50, así que el resultado sería: 99x50=4950, a falta de sumar el número 100, que es el que falta, entonces:
99 x 50 + 100 = 5050
Otro método
Este método que os cuento ahora, es un método que conocí hace unos 10 años para sumar los 100, 1000 ó 10000 primeros números naturales, incluso mentalmente. Con el ejemplo del 100, es así:
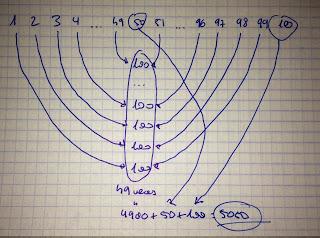Suma de los 100 primeros números. Créditos: A. Pérez Verde.
Sumamos 1+99, 2+98, 3+97, ... hasta llegar a la mitad menos uno del número en cuestión, en este caso, 100/2-1=49, por lo tanto, tendríamos 49 veces 100, que sería 4900, sumado con el 50 del centro, hacen 4950, más el 100: 5050.
49 x 100 + 50 + 100 = 5050
Cuenta la leyenda que este método lo descubrió Gauss. En clase, como castigo le impusieron que sumara los 100 primeros números para que dejara de hablar y su profesor pensó que le llevaría varios minutos hacerlo, pero la sorpresa fue mayúscula cuando vio que lo resolvío en apenas unos segundos por este método.
Seguramente haya muchos más métodos. Si sabéis alguno más, os invito a que lo resumáis en los comentarios.
--¿Te interesa? Sígueme también en Twitter.
¿Te gusta mi blog? Vótalo en los Bitácoras 2012.