¿Y a qué viene tanto recordatorio? Pues a que Miguel Ángel, que también es editor del Boletín de la RSME, presentó la semana pasada el 39º Desafío Matemático titulado Dos segmentos iguales y en ángulo recto:
Aquí os dejo la transcripción del problema:
Partiendo de un triángulo cualquiera de vértices ABC, tomamos dos de sus lados, AB y AC por ejemplo, y dibujamos cuadrados apoyados en ellos. Llamamos I y J a los centros de los dos cuadrados y H al punto medio del lado del triángulo donde no hemos apoyado ningún cuadrado (el BC en este caso).Bueno, pues como no podía ser de otra forma, desde Tito Eliatron Dixit no podíamos permitir que otro blog de matemáticas nos lanzara descaradamente un guante así y no recogerlo. Así que en cuanto tuve un minutito, me puse a resolverlo y aquí os traigo mi propuesta de solución.
El desafío de esta semana consiste en demostrar que los segmentos HI y HJ tienen la misma longitud y que además forman un ángulo de 90º (ver imagen original).
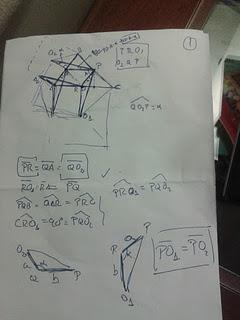
Vale, este fue mi primer intento y, en realidad, si os fijáis bien, ahí está todo resuelto. Sin embargo, al poco me dí cuenta de que este método dependía del ángulo en el que estuvieran los lados sobre los que se levantaban los cuadrados (si era agudo, recto u obtuso, había que variar ligeramente la argumentación). Así que finalmente, me decidí a atacarlo usando geometría analítica, partiendo de algunas simplificaciones previas. Veamos la solución.
Sin pérdida de generalidad (haciendo giros y traslaciones), podemos suponer que el vértice
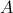 común a los dos lados sobre los que se levantan los cuadrados es el origen de coordenadas; que uno de los otros vértices
común a los dos lados sobre los que se levantan los cuadrados es el origen de coordenadas; que uno de los otros vértices 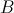 , está en el semieje positivo de abscisas, es decir, tiene por coordenadas
, está en el semieje positivo de abscisas, es decir, tiene por coordenadas 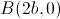 con
con 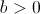 ; y que el tercer vértice
; y que el tercer vértice 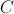 , está en el semiplano superior, es decir, podemos suponer que
, está en el semiplano superior, es decir, podemos suponer que 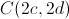 con
con 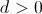 (lo de escribir
(lo de escribir 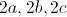 es por cuestiones técnicas, para que no me salgan fracciones al final, vamos). Veámoslo mejor, en el siguiente dibujo.
es por cuestiones técnicas, para que no me salgan fracciones al final, vamos). Veámoslo mejor, en el siguiente dibujo.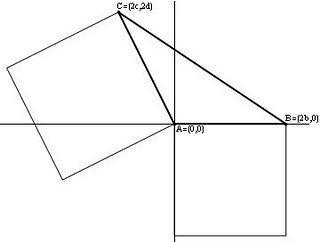
El centro
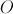 del cuadrado que se levanta sobre el lado
del cuadrado que se levanta sobre el lado  es, obviamente,
es, obviamente, 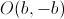 . Para hallar el centro del cuadrado que se levanta sobre el lado
. Para hallar el centro del cuadrado que se levanta sobre el lado 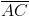 , vamos a calcular el vértice
, vamos a calcular el vértice 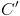 opuesto en el cuadrado a
opuesto en el cuadrado a 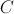 . Para ello, como el vector
. Para ello, como el vector 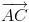 debe ser perpendicular a
debe ser perpendicular a 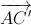 y como
y como 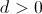 , debe ser
, debe ser 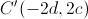 . Así, el centro
. Así, el centro 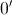 del cuadrado será el punto medio del segmento
del cuadrado será el punto medio del segmento 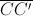 , es decir,
, es decir, 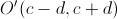 . Además, el punto medio
. Además, el punto medio 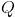 del segmento
del segmento 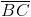 será
será 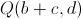 . Todo esto se ve en la siguiente imagen.
. Todo esto se ve en la siguiente imagen.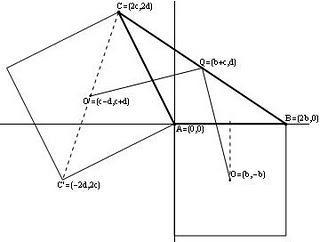
Así pues, se tiene que
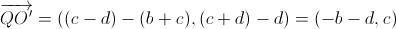
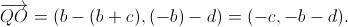 Luego
Luego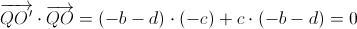 y se tiene que
y se tiene que 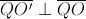 .
.Además,
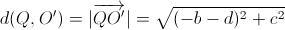 , mientras que
, mientras que 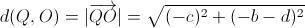 , por lo que es evidente que
, por lo que es evidente que 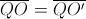 .
.Y esto es todo. Supongo que este problema se podrá atacar de muchas formas diferentes, como casi todos los problemas geométricos. Al final, aposté por la claridad en las cuentas, antes que por la simplicidad de los argumentos. Realmente, los conceptos que se usan en la imagen de mi manuscrito son bastante simples (semejanzas de triángulos e igualdades de ángulos), pero hay que hilar más fino. Sin embargo, la solución que propongo hace uso del producto escalar y la geometría analítica que, aunque no es demasiado complicado, sí es una herramienta más potente que lo anterior, lo cual,m entre otras cosas, hace que las cuentas y los cálculos sean bastante simples (si tenemos las precauciones previas de colocar el triángulo adecuadamente).
Tito Eliatron Dixit
Si te ha gustado esta entrada, puedes dejar un comentario directamente en Tito Eliatron Dixit.

