Dynamic Time Warping

Hoy hablaré de esta técnica de una manera sencilla, ya que en la mayoría de las explicaciones disponibles en la web, meten un montón de fórmulas y de explicaciones difíciles de entender.

Primeramente la definición

DTW  es un algoritmo para medir la similaridad entre dos secuencias, mismas que pueden variar en el tiempo o velocidad.

Para dejar más claro lo anterior, agrego la siguiente figura:

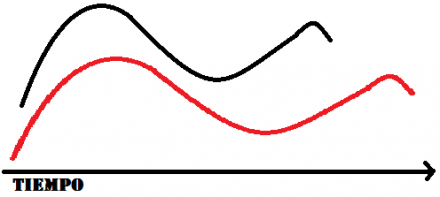
Supongamos que las curvas roja y negra representan dos señales de algún tipo, por decir un ejemplo, digamos que es sonido. Como puede observarse, ambas señales son la misma, con la diferencia de que una de ellas tiene mayor duración que la otra (supongamos que alguien dijo ‘hola’ lentamente y después dijo ‘hola’ con una velocidad normal, la señal será parecida pero con duración distinta), pero ambas presentan el mismo comportamiento: al inicio hay una curva grande hacia arriba, y después una curva grande hacia abajo, para finalizar con una pequeña curva hacia arriba al final.

Si tratamos de comparar estás dos señales con un algoritmo simple (comparando el 1er punto de la señal 1 con el 1er punto de la señal 2, el 2do punto de la señal 1 con el 2do punto de la señal 2, y así sucesivamente), el resultado será que la computadora detectará dos señales distintas (cuando son la misma con una ligera variación).

DTW nos permite estirar y encoger ambas señales para tratar de hacerlas coincidir lo mejor posible, de esta manera, si presentan el mismo patrón ambas señales, el algoritmo logrará reconocerlas con mayor exactitud.

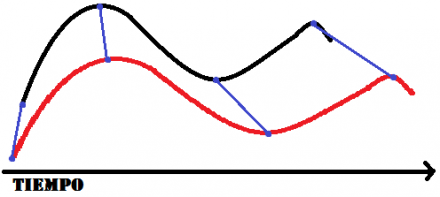
Como se ve en la figura de arriba, el algoritmo tratará de encontrar las coincidencias entre ambas señales.

Ahora supongamos que tenemos las siguientes señales, utilizaré numeros enteros para hacerlo más sencillo:

S1= 1 1 1 2 2 1 3 3 5

S2= 1 1 2 1 3 5

Vemos que la señal 1 (S1) es más larga que la señal 2 (S2), aún asi, hay manera de ajustar ambas señales. Para hacerlo haremos uso de una matriz de tamaño n x m, donde n es la longitud de S1 y m la longitud de S2, para el ejemplo anterior, tendremos una matriz de 9×6. En esta matriz almacenaremos la distancia de cada uno de los puntos de S1, hacia cada uno de los puntos en S2, esto lo haremos restando los puntos de S1 y S2:

Continuará…