Ejercicios resueltos sobre Intervalos de confianza para la media de una población

“Un Intervalo de confianza es un conjunto de valores formado a partir de una muestra de datos de forma que exista la posibilidad de que el parámetro poblacional ocurra dentro de dicho conjunto con una probabilidad específica. La probabilidad específica recibe el nombre de nivel de confianza.” Lind, Douglas. (2008), Estadística Aplicada a los Negocios y la Economía, México D.F., México, McGraw-Hill/Interamericana Editores, S.A.

Para establecer un intervalo de confianza para la media de una población determinada utilizaremos una de dos distribuciones: distribución normal estándar o distribución t de Student, cada una de ellas se utilizará en función de los supuestos que se hagan de la población investigada, de la información que de ella se tenga y del tamaño de la muestra elegida.
Un detalle importante es conocer el significado práctico del término Nivel de confianza, por ejemplo, un nivel de confianza de 95% significa que el 95% de las observaciones estarán ubicadas en el centro de la distribución y el 5% restante se ubicarán en partes iguales en “las colas” de la distribución, esto es, 2.5% a cada lado.


En el caso de la distribución t de Student, el principio es el mismo y más adelante veremos un ejemplo de como leerla. 

Ahora resolvamos algunos ejemplos: 

Intervalo de confianza para la media de una población con Desviación Estándar conocida – Muestras Grandes (n > 30). 

Una empresa de investigación llevó a cabo una encuesta para determinar la cantidad media que los fumadores gastan en cigarrillos durante una semana. La empresa encontró que la distribución de cantidades gastadas por semana tendía a seguir la distribución normal, con una desviación estándar de $5. Una muestra de 49 fumadores reveló que . 
a. ¿Cuál es el estimador puntual de la media de la población? 
Según la muestra tomada $20 es la estimación de la media poblacional. 
b. Con el nivel de confianza de 95%, determine el intervalo de confianza para 𝞵

Intervalo de confianza para la media de una población con Desviación Estándar desconocida – Muestras Grandes (n > 30).

Cuando desconocemos la desviación estándar de la población (en la vida real es lo más probable) si el tamaño de muestra es lo suficientemente grande (n ≥ 30), el teorema del Límite Central nos permite utilizar la distribución normal como la distribución de muestreo, teniendo en cuenta lo siguiente: 

Jon Jackobsen, un pasante de posgrado muy dedicado, acaba de terminar una primera versión de su tesis de 700 páginas. Jon mecanografió el trabajo por sí mismo y está interesado en conocer el número promedio de errores tipográficos por página, pero no quiere leer todo el documento. Como sabe algo acerca de estadística para la administración, Jon leyó 40 páginas seleccionadas de manera aleatoria y encontró que el promedio de errores tipográficos por página fue de 4.3 y la desviación estándar de la muestra fue de 1.2 errores por página.a. Calcule el error estándar estimado de la media.

b.Calcule un intervalo de confianza del 90% para el número promedio verdadero de errores por página en su trabajo.

Intervalo de confianza para la media de una población con Desv. Estándar desconocida – Muestras Pequeñas (n < 30).

Para este caso particular utilizaremos la distribución t de Student con n -1 grados de libertad:

El propietario de Britten’s Egg Farm desea calcular la cantidad media de huevos que pone cada gallina. Una muestra de 20 gallinas indica que ponen un promedio de 20 huevos al mes, con una desviación estándar de 2 huevos al mes.a.     ¿Cuál es el valor de la media de la población? ¿Cuál es el mejor estimador?
No se conoce la media poblacional, pero su mejor estimador es huevos al mes.
b.  Explique por qué necesita utilizar la distribución t. ¿Qué suposiciones necesita hacer? Utilizamos la distribución t porque se desconoce la desviación estándar de la población, pero para aplicarla, debemos suponer que la población sigue una distribución normal.
c. ¿Cuál es el valor t para un intervalo de confianza de 95%?

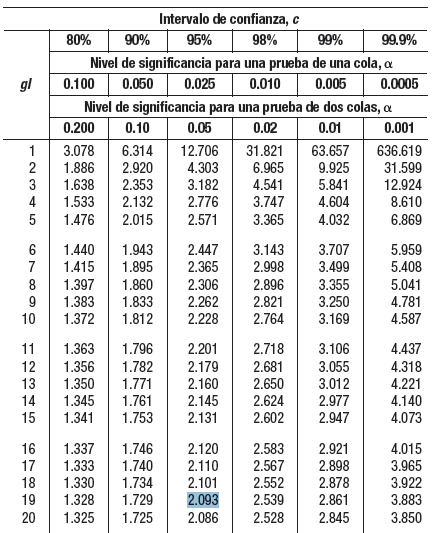
Con 95% de confianza y n – 1 = 20 – 1 = 19 grados de libertad, entonces, t = 2.093

d. Construya un intervalo de confianza de 95% para la media de la población.



En nuestra página de descargas puedes obtener un archivo en formato PDF con los ejercicios aquí resueltos. 
Si necesitas reforzar conocimientos o estudiar para el examen que se acerca, resolución de tareas, proyectos con SPSS, Minitab, etc., puedes comunicarte conmigo al 0980700611 (whatsapp/llamadas).