Ejercicios resueltos utilizando la Distribución de Probabilidad Geométrica

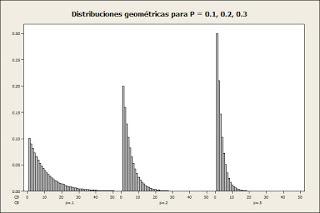
Una de las distribuciones discretas de probabilidad más conocida es la  distribución Geométrica, se presenta como un modelo adecuado para aquellos procesos donde se repiten  pruebas hasta obtener un "éxito" o "resultado deseado". En uno de nuestros artículos anteriores puede recordar algunas de las características de esta distribución.

Si lo que se requiere es encontrar la probabilidad de que se realicen x ensayos hasta obtener un éxito, entonces la Distribución Geométrica está representada por:
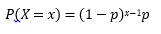Para x = 1, 2, 3, ...
Si lo que se requiere es encontrar la probabilidad de que existan x fallos hasta obtener el primer éxito, entonces la Distribución Geométrica está representada por:

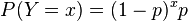
Para y = 0, 1, 2, ...

Ahora sí resolvamos algunos ejemplos:
Si la probabilidad de que un cierto dispositivo de medición muestre una desviación excesiva ws de 0.05, ¿cuál es la probabilidad de que:
a) El sexto de estos dispositivos de medición sometidos a prueba sea el primero en mostrar una       desviación excesiva .
b) El quinto de estos dispositivos de medición sometidos a prueba, sea el primero que no                muestre una desviación excesiva.

a) Sea:
    x = 6 - El sexto dispositivo sea el primero que muestre una variación excesiva.
    p = 0.05 - La probabilidad de que un dispositivo de medición muestre una variación excesiva.
 

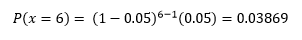
b) Sea:
    x = 5 - El quinto dispositivo sea el primero que muestre una variación excesiva.
    p = 0.95 - La probabilidad de que un dispositivo de medición no muestre una variación excesiva.

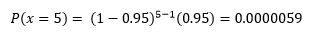
Los registros de una compañía constructora de pozos, indican que la probabilidad de que uno de sus pozos nuevos, requiera de reparaciones en el término de un año es de 0.20. ¿Cuál es la probabilidad de que el quinto pozo construido por esta compañía en un año dado sea el primero en requerir reparaciones en un año?

Sea:
x = 5 - El quinto pozo sea el primero que requiera reparaciones en un año.
p= 0.20 - La probabilidad de que un pozo requiera reparaciones en el término de una año.

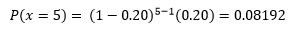
La probabilidad de que cierto análisis clínico dé una reacción positiva es 0.04. Los resultados de los análisis son independientes unos de otros ¿Cuál es la probabilidad de que la primera reacción positiva ocurra antes del tercer análisis?

Aquí el éxito radica en obtener una reacción positiva antes del tercer análisis, lo que indica que puede ocurrir en el primer intento o en el segundo. Por tanto la probabilidad deseada estará dada por:
P(x < 3) = P(x=1) + P(x=2)

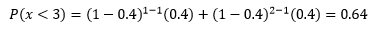
Se tienen 4 llaves de las cuales sólo una abre un  candado. Se prueban las llaves una tras otra, con reemplazo, hasta encontrar la que abre el candado. Calcular la probabilidad de que el candado se abra después del segundo intento.
En este ejercicio no nos indican cual es la probabilidad de que una determinada llave abra el candado, pero calcular dicho valor es muy sencillo: dado que hay cuatro llaves y una de ellas abre el candado, entonces la probabilidad p de que una llave abra el candado será 1/4 = 0.25. Además, dado que queremos calcular la probabilidad de que el candado se abra después del segundo intento entonces x = 3, 4, 5, ... dicho de otra manera:
P(x>2) = 1 - P(x <= 2) = 1 - [P(x=1) + P(x=2)]

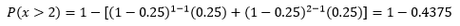
P(x>2) = 0.5625

Tres personas lanzan una moneda y el disparejo paga el café. Si los tres resultados son iguales, las monedas se lanzan nuevamente. Encontrar la probabilidad de que se necesiten menos de cuatro intentos para saber quien paga el café.
En este problema el éxito consiste en sacar el disparejo. Lo primero que debemos hacer para resolver el problema es encontrar el espacio muestral correspondiente al lanzamiento de las 3 monedas:
S = {(c, c, c) (c, c, +) (c, +, c) (+, c, c) (c, +, +) (+, c, +) (+, +, c) (+, +, +)}
Donde: "c" = cara y "+" = sello
Podemos apreciar que la magnitud del espacio muestral es 8 y que es un espacio equiprobable. El número de resultados en que aparece el "disparejo" es 6, por lo que p = 6/8 = 0.75.
Si queremos obtener la probabilidad de que se necesiten menos de 4 intentos para saber quien paga el café, entonces:
P(x<4) = P(x=1) +  P(x=2) +  P(x=3)  


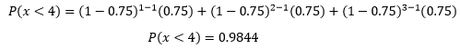
Puedes descargar un documento PDF con los ejercicios aquí resueltos desde la página de descargas. 
Si necesitas clases o realizar algún proyecto que implique estadística puedes contactarme al 0980700611.