Ejercicios resueltos utilizando una Distribución de Probabilidad Binomial Negativa.

La distribución binomial negativa o distribución de Pascal puede definirse como una generalización de la distribución de probabilidad geométrica donde la variable aleatoria X es el número de ensayos Bernoulli efectuados hasta que se tienen r éxitos, con una probabilidad constante de éxito p. Se dice entonces que X tiene una distribución binomial negativa con parámetros p y r = 1, 2, 3,...


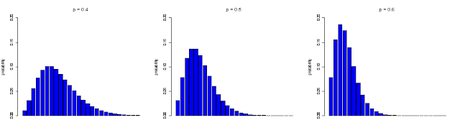
Nótese que el caso de que r = 1, tenemos el caso de una distribución de probabilidad geométrica.

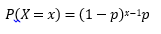
Una aeronave tiene 3 computadoras idénticas. Sólo una de ellas se emplea para controlar la nave, las otras 2 son de reserva, redundantes, por si falla la primera. Durante una hora de operación la probabilidad de fallo es 0.0005. 
a.- ¿Cuál es el tiempo promedio de fallo de las tres computadoras?

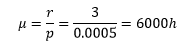
b.- ¿Cuál es la probabilidad de que las 3 fallen durante un vuelo de 5 horas?

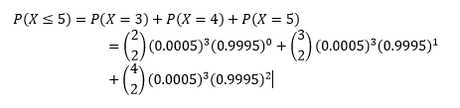
Sí la probabilidad de que un cierto dispositivo de medición muestre una desviación excesiva es de 0.05, ¿cuál es la probabilidad de que; a) el sexto de estos dispositivos de medición sometidos a prueba sea el tercero en mostrar una desviación excesiva?, b) el séptimo de estos dispositivos de medición sometidos a prueba, sea el cuarto que no muestre una desviación excesiva.




Los registros de una compañía constructora de pozos, indican que la probabilidad de que uno de sus pozos nuevos, requiera de reparaciones en el término de un año es de 0.20. a) ¿Cuál es la probabilidad de que el sexto pozo construido por esta compañía en un año dado sea el segundo en requerir reparaciones en un año?

b) ¿Cuál es la probabilidad de que el octavo pozo construido por esta compañía en un año dado sea el tercero en requerir reparaciones en un año?

Espero que te sirvan a manera de ejemplo estos ejercicios, en nuestra página de descargas puedes obtener un archivo en formato PDF con los ejercicios aquí resueltos. Si necesitas reforzar conocimientos o estudiar para el examen que se acerca puedes comunicarte conmigo al 0980700611 (whatsapp/llamadas).