




Un jugador ha sido asesinado en los vestuarios, en el descanso de un partido del Mundial de Brasil 2014. Una serie de pistas matemáticas te conducirán a resolver el misterio, con la ayuda del inspector Larry Flanagan y del agente Pepe Vitruvio, que te introducirán en el fascinante mundo de la Combinatoria.
¿Te atreves a resolver el caso?


(Esta entrada participa en la Edición 5.5: Ronald Fisher del Carnaval de Matemáticas, cuyo anfitrión es el blog pimedios.)

El asesino matemático
Nadie podía creérselo. Estaban esperándole para comenzar la segunda parte del encuentro, pero no acababa de salir al terreno de juego. Finalmente, el preparador físico bajó a los vestuarios para ver qué es lo que ocurría y se lo encontró allí, tendido en el suelo, con un puñal clavado en el pecho.

Era Drakulic, el delantero centro y capitán de la selección de Transilvania, que se había clasificado brillantemente por primera vez para los Mundiales de Fútbol, que este año se celebraban en Brasil.
Ninguno de los jugadores recordaba quién había sido el último en abandonar el vestuario, ya que estaban todos bastante afectados por la charla que les había dado el seleccionador, Pep Touriño, tras ir perdiendo en el descanso por 2 goles a 0 con la selección de Micronesia Occidental.

Los organizadores del Campeonato querían que el asunto se aclarase con la mayor rapidez y discreción posible, por lo que solicitaron a la Policía que les enviasen a los mejores agentes, para poder resolver el caso cuanto antes.
En escasos minutos, se presentaron en el estadio el inspector Larry Flanagan, y Pepe Vitruvio, oficial del Departamento de Matemática Científica de la Policía.

¿Por qué fueron ellos los escogidos? Bueno, Larry Flanagan (F) era el más brillante inspector del cuerpo. Pero no sabía mucho de Matemáticas.
La colaboración de un agente del Departamento de Matemáticas parecía fundamental, ya que, insertados en el puñal, había tres recortes del periódico de hoy, todos ellos relacionados con el partido que iban a disputar, y con una serie de anotaciones matemáticas escritas en los mismos.
Además, los recortes de las noticias no tenían la tradicional forma rectangular, sino que estaban cortados en forma de triángulo, y estaban atravesados por el puñal por su mismo centro.

Todo parecía indicar que el autor del asesinato se trataba de una persona aficionada a las Matemáticas, y que, además, había ido dejando una serie de pistas cuya resolución les conduciría hasta él.
Por tanto, la intervención de Pepe Vitruvio (V) parecía imprescindible para resolver el caso, ya que era un experto en la resolución de este tipo de enigmas.
El inspector se puso manos a la obra. Echó mano a los recortes, y leyó el primero de ellos, que decía así: ‘Para el partido de esta tarde, nuestro seleccionador duda qué pareja de centrales alineará de entre los 4 que tiene disponibles’. En la parte superior del recorte, figuraba una misteriosa anotación en rojo: (4 2).

F: No entiendo qué relación puede tener esta noticia de los defensas con el jugador asesinado, que es delantero. Y además, ¿qué significarán esos números en rojo, 4 y 2, escritos uno debajo del otro, y entre paréntesis? – Dijo el inspector Larry Flanagan.
V: Podría tratarse de una anotación matemática, un coeficiente binomial, que representa las combinaciones de 4 elementos tomados de 2 en 2. En este caso, puede indicar el número de posibles combinaciones de 2 centrales que puede hacer el seleccionador si cuenta con 4 jugadores que pueden jugar en esa posición. Como diríamos en nuestro Departamento, las combinaciones (sin repetición) son el número de subconjuntos de k elementos que se pueden extraer de un conjunto dado de n elementos. – Explicó Pepe Vitruvio.
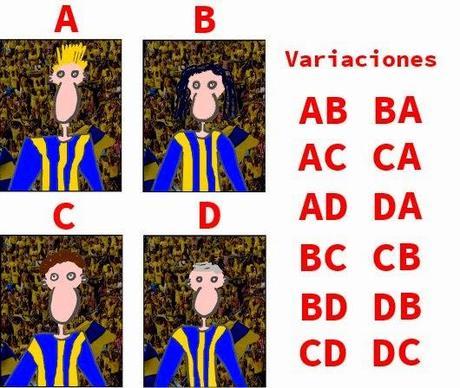
F: Ya veo. Si tenemos 4 jugadores, a los que llamaremos A, B, C y D (los nombres transilvanos son realmente complicados, así que será mejor utilizar las letras), el seleccionador podrá escoger las siguientes parejas: AB, BC, CD, AC, BD y AD. Esto es, un total de 6 parejas distintas, ¿verdad?

V: Cierto. Eso siempre que no nos importe en qué posición jueguen. Esto es, que nos da lo mismo si cada uno de ellos juega en la izquierda o en la derecha de la defensa. De no ser así, tendríamos un total de 12 combinaciones, ya que deberíamos contar con las mismas parejas, pero cambiando el orden: BA, CB, DC, CA, DB, y DA. En este caso, hablaríamos de variaciones (sin repetición) de 4 elementos tomados de 2 en 2, y no de ‘combinaciones’.
F: Bien, pues parece que la primera pista nos conduce al número 6. Vamos a ver el siguiente recorte: ‘Indignación en Brașov. Tras la buena temporada del Sporting de Brașov, el seleccionador sólo alineará a 2 jugadores de los 7 del equipo que se llevó a Brasil’. También en este recorte alguien había escrito un 7 y un 2, entre paréntesis y uno debajo del otro.

F: No me lo digas, Pepe. Creo que esta vez lo he pillado: la anotación (7 2) representa las posibles combinaciones de 7 elementos tomados de 2 en 2, que puede hacer el seleccionador. Esto es, el número de posibles parejas distintas de jugadores del Sporting que el entrenador puede escoger para que jueguen el partido. ¿Me equivoco?
V: No, inspector Larry. Veo que aprendes muy deprisa.
F: Vale, vamos a ver cuáles pueden ser. Si tenemos 7 jugadores, a los que llamaremos con las letras A, B, C, D, E, F y G, las combinaciones serán: AB, FE, AC, CD, AD, BD, CF...
F: ¡Uy! Creo que me he perdido. Ahora no es tan fácil calcularlas... Voy a comenzar otra vez, de una forma más ordenada: AB, AC, AD, AE....
Tras un rato, el inspector llegó al resultado:
AB AC AD AE AF AG BC BD BE BF BG CD CE CF CG DE DF DG EF EG FG
F: Creo que son 21, pero no estoy seguro de si me he olvidado de alguna…
V: Sí, es correcto. Aunque en este caso, sería mejor acudir a las Matemáticas. La fórmula para hallar las combinaciones de k elementos tomados un conjunto de n elementos, es la siguiente:

F: ¿De dónde sale esa fórmula?
V: Bueno, pensemos en el primer jugador que puede escoger el entrenador. Está claro que hay 7 posibles candidatos, los 7 jugadores del Sporting. Cuando quiera elegir al segundo jugador, ya sólo tendrá 6 jugadores entre los escogerlo, ¿verdad? Por tanto, para cada uno de los siete jugadores elegidos inicialmente, habrá seis posibles compañeros. Así que tenemos 7 x 6 = 42 posibles parejas:
AB AC AD AE AF AG BA BC BD BE BF BG CA CB CD CE CF CG DA DB DC DE DF DG EA EB EC ED EF EG FA FB FC FD FE FG
V: Pero en este caso volvemos a obtener las variaciones de 7 elementos tomados de 2 en 2, ya que tenemos parejas repetidas: AB y BA, por ejemplo. Y hemos quedado que nos da igual la posición en la que jueguen ¿Qué podemos hacer para eliminarlas de nuestra fórmula?
F: No se me ocurre..
V: Deberíamos dividir el resultado entre el número de formas posibles en que podemos encontrar la misma combinación de jugadores, aunque ordenada de distinta manera. Es lo que en nuestro Departamento llamamos ‘permutaciones’ (sin repetición): el número de distintas ordenaciones que podemos hacer en un conjunto de elementos, utilizando todos los números, pero sin que se repitan.
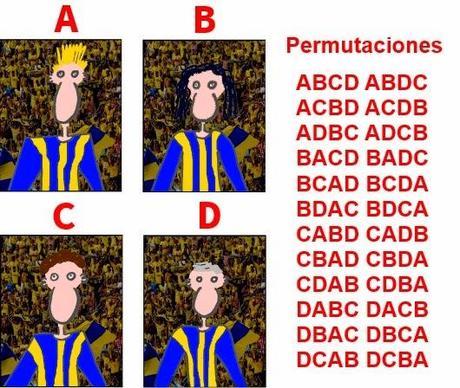
F: ¿Y cómo calculamos el número de permutaciones?
V: Es muy sencillo: Si tenemos k elementos, debemos pensar que cualquiera de ellos puede ser el primero. Después, habrá (k-1) elementos que puedan estar en segundo lugar (ya que no se pueden repetir). Habrá (k-2) elementos que puedan estar en tercer lugar. Y así sucesivamente. El total de formas distintas en que pueden ordenarse k elementos será igual a
P(k) = k • (k-1) • (k-2) • … • 3 • 2 • 1
V: En nuestro Departamento no nos gusta perder el tiempo escribiendo este tipo de fórmulas tan largas, así que hemos inventado para definir es producto la clave secreta ‘factorial de k’, que escribimos así: k! Por tanto, podemos escribirlo de esta manera:
P(k) = k!
V: Para nuestro caso concreto con conjuntos de 2 jugadores, tendremos que k! = 2! = 2 • 1 = 2
V: Así que ya tenemos el resultado para nuestro problema. Para obtener las combinaciones de 2 elementos tomados de un total de 7, dividimos las variaciones de 7 elementos tomados de 2 en 2 entre las permutaciones de 2 elementos:

F: Eso es lo que yo dije al principio, sin tanta fórmula!
V: Es verdad, pero te costó bastante obtener el número. Y eso que sólo eran 7 jugadores. ¿Qué habría ocurrido si hubieras tenido que escoger, por ejemplo, a 5 jugadores de entre los 23 seleccionados? ¿Habrías escrito todas las posibles combinaciones?
F: Hummm… Bien, de acuerdo. Prosigue con tu explicación, por favor.
V: Vamos a modificar ahora ligeramente la fórmula anterior, multiplicando el numerador y el denominador por 5!

V: Hemos llegado a la fórmula que te indiqué inicialmente, ¿lo ves?

F: Correcto. Pero empiezo a estar harto de tantos números, tantas variaciones, combinaciones, permutaciones… Creo que lo mejor sería tomar las huellas dactilares del puñal, y asunto arreglado.
V: Inspector, ya sabes que los asesinos suelen utilizar guantes en estos casos… Además, con motivo de la celebración del Mundial, el personal del Laboratorio está bajo mínimos. Y sabemos que no se distinguen precisamente por la rapidez de sus análisis.
F: De acuerdo. Sigamos con la investigación. Vamos a por el tercer recorte: ‘Hoy se prevé una lucha importante en el centro del campo, así que el seleccionador dice que alineará a 5 de los 7 mediocampistas que se ha llevado al Mundial.’ Encima de la noticia se puede leer una nueva anotación (7 5).

F: Bueno, pues ahora tenemos la combinación de 7 jugadores tomados de 5 en 5, ¿verdad? Vamos a calcularlo con la fórmula que me has enseñado.
V: También da 21.
F: ¿Cómo lo has calculado tan rápido?
V: En realidad no he realizado ningún cálculo. Tenemos que

V: En términos generales,
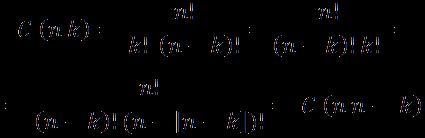
F: ¿Y por qué da el mismo resultado?
V: Bien, piensa que el problema de calcular las combinaciones posibles de 5 jugadores si tenemos 7 en total se puede plantear de otra forma. Podemos pensar en los 2 jugadores que se quedan en el banquillo cada vez que el seleccionador escoge a 5 de ellos para jugar.
ABCDE – FGABCDF – EGABCEF – DGABCEG – DF…
V: Así que a cada grupo de 5 jugadores seleccionados le corresponde un grupo de 2 jugadores no seleccionados. Habrá tantos grupos distintos de 5 jugadores elegidos para jugar como grupos de 2 jugadores que se quedan en el banquillo.
V: Por tanto, en vez de calcular cuántos grupos de 5 jugadores titulares se pueden formar, podemos ver cuántos grupos de 2 jugadores suplentes puede haber, si contamos con 7 jugadores en total, ya que la solución será la misma. Y como en el recorte anterior ya habíamos calculado que había 21 posibles combinaciones para dicho caso, esta vez no necesitamos echar ningún cálculo.
F: Perfecto. Ahora solo nos queda encajar las piezas con las que contamos. Los resultados de los 3 paréntesis misteriosos (4 2),(7 2) y (7 5) han resultado ser los números 6, 21 y 21. Yo creo que si el puñal atravesaba los tres recortes por su mismo centro, quizás lo que deberíamos hacer sería hallar el ‘centro’ aritmético de los números obtenidos, esto es, su media:
 F: ¡Vaya, 16! ¡Justo el número que luce como dorsal el jugador asesinado!
F: ¡Vaya, 16! ¡Justo el número que luce como dorsal el jugador asesinado! 
F: Está claro que el asesino es un aficionado a las Matemáticas y a los problemas de lógica, y que además no nos lo va a poner nada fácil. Y ahora, Pepe, ¿qué hacemos?
V: Todavía hay un dato que no hemos utilizado en nuestra investigación, quizás el más evidente de todos: los recortes presentan una forma triangular.
V: Si el asesino es un experto en Matemáticas, y además todos los problemas que hay en los recortes son sobre la rama de Combinatoria, sin duda todo nos conduce al triángulo de Pascal. ¿Conoces este triángulo, Flanagan?
F: No, no sé qué es eso.
V: Bueno, es normal. Este triángulo, al igual que los criminales más astutos, adopta un montón de personalidades distintas. Por ejemplo, también se le conoce por triángulo de Tartaglia. En todo caso, y volviendo al tema que nos ocupa, te diré que se trata de un triángulo de confección muy sencilla. Primeros escribimos un 1 en el vértice superior, y debajo, sucesivamente y en diagonal, escribimos el resultado de sumar los dos números situados encima. Si no hay ningún número, sumamos un cero.

V: Ahora vamos a señalar en este triángulo de Pascal los resultados obtenidos. Fíjate, inspector. En el primer caso (4 2), si cogemos la quinta fila (prescindimos del primer 1 solitario) y nos vamos hasta el tercer número, obtenemos el valor de 6. El mismo resultado que utilizando nuestra fórmula.
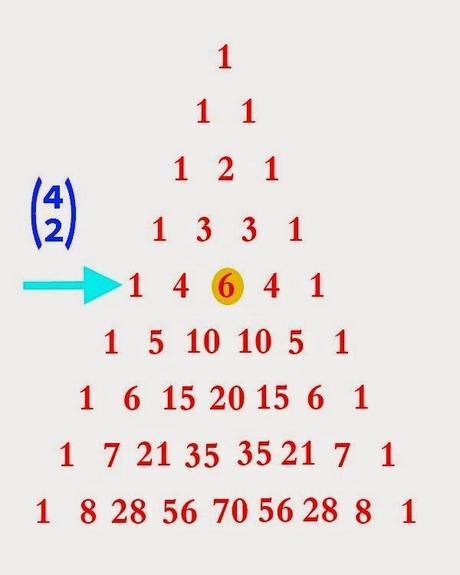
F: ¿Por qué has señalado el tercer número de la quinta fila, y no el segundo número de la cuarta fila?
V: Porque el vértice del triángulo corresponde al coeficiente binomial (0 0). Y, en cada línea n, el primer número representa la combinación (n 0). Así, en nuestra quinta línea (4 0) es igual a 1, (4 1) es igual a 4, (4 2) es igual a 6, y así sucesivamente. ¿Comprendido?
F: Sí. No pensé en el número 0.
V: Ahora haremos lo mismo con el (7 2) y con el (7 5). Puedes comprobar que los números forman un precioso triángulo, similar en forma a los recortes de periódico.

F: Y como el triángulo es simétrico, ahora entiendo por qué (7 2) es igual que (7 5).
V: Estupendo. Ahora sólo nos queda señalar el número que se encuentra en el centro geométrico del triángulo que hemos formado, que es justo el lugar por el que el puñal atravesaba los recortes. Y obtenemos el número 20.

F: ¿A qué jugador corresponde dicho número? ¡Que le traigan aquí inmediatamente! – Gritó el inspector Larry Flanagan.
Se trataba de Vladimiric. La policía no tardó en encontrarle dentro del estadio, y lo acercó hasta el vestuario.

Allí Vladimiric confesó su crimen. Era amigo de Drakulic desde la infancia. Desde bien pequeños Drakulic le había superado en todo: tenía mejor expediente académico, ligaba mucho más, tenía más amigos y jugaba mejor al fútbol. De hecho, Drakulic era el capitán de la selección de Transilvania, y Vladimiric era suplente, apenas si jugaba un par de minutos en algunos partidos. Pero ninguno de estos motivos había sido la causa que había desencadenado el fatal desenlace.
F: Y entonces, ¿por qué lo has hecho? - Preguntó Larry Flanagan.
Bien, dijo Vladimiric, había sólo un par de asuntos en los que Drakulic nunca me había superado: en las Matemáticas y en los problemas de Lógica. Al menos hasta hoy... Cuando veníamos en el autobús desde el hotel de concentración hasta el estadio, hicimos una apuesta sobre quién resolvería antes el sudoku del periódico. Y por primera vez en la vida, Drakulic ha sido más rápido que yo. No pude soportarlo...

Si te gustó esta historia, puedes votar por ella en menéame y divoblogger. Muchas gracias.
