El triángulo evanescente

That there, that’s not me
I go where I please
I walk through walls
I float down the Liffey

I’m not here
This isn’t happening
I’m not here, I’m not here

In a little while
I’ll be gone
The moment’s already passed
Yeah, it’s gone

I’m not here
This isn’t happening
I’m not here, I’m not here

Radiohead “How To Disappear Completely”

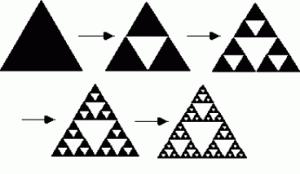
Consideremos un triángulo equilátero, lo dividimos en cuatro triángulos equiláteros iguales, y eliminamos del conjunto el triángulo central. Esta operación la repetimos una y otra vez con los triángulos equiláteros que van apareciendo en el proceso, y así es como se construye un triángulo de Sierpenski, o quizás sería mejor decir, como se desvanece el triángulo del que partíamos (que podíamos suponer hecho de algún material de espesor infinitesimal).

Esta construcción es debida al matemático polaco Wacław Franciszek Sierpiński (de ahí el nombre), nacido el 14 de marzo de 1882 en Varsovia, y fallecido el 21 de octubre de 1969 en la misma ciudad. Sierpinski hizo importantes contribuciones a la teoría de conjuntos y la lógica, la topología y la teoría de números, cosechando en esta última materia un premio por su primer trabajo aún como estudiante. Aunque coemnzó a dar clases de matemáticas y física, el cierre de su escuela le animó a tomar la decisión de realizar un doctorado en la prestigiosa universidad de Cracovia.

Wacław Sierpiński

Sierpinski fue un matemático muy prolífico, y se cuentan más de 700 artículos y unos 50 libros, lo que en matemáticas es simplemente excepcional. Fue profesor en la universidad de Lwow desde 1908, pero con la primera guerra mundial le obligó a marcharse a Moscú, donde fue internado debido al uso político de rusos y austríacos de la cuestión polaca. Los matemáticos rusos Egorov y Luzin consiguieron liberarlo y allí trabajó con Luzin. Volvió a Lwow al terminar la guerra, y en 1919 se trasladó a Varsovia hasta su fallecimiento.

Sierpinski sufrió de nuevo la bestialidad de la guerra con la segunda guerra mundial, y aunque siguió trabajando en la universidad, su trabajo oficial era de bedel. Su casa fue quemada en 1944, perdiendo sus libros y su correspondencia personal. Es dramático como describió estos horrores, con los asesinatos de sus estudiantes, en una conferencia que impartió en Cracovia en 1945. Sierpinski había fundado la revista polaca mas prestigiosa, Fundamenta Mathematicae; durante la guerra el siguió trabajando enviando sus artículos a Italia, y escribiendo al final de cada uno: “Las demostraciones de estos teoremas aparecerán publicadas en Fundamenta Mathematicae”, lo que todos interpretaban como “Polonia sobrevivirá”.

Wacław Sierpiński describió su triángulo en 1915, aunque históricamente este patrón se encontraba en los mosaicos Cosmati de siglo XIII en la catedral de Anagni en Italia, así como en la Basílica Romana de Santa María en Cosmedin, y también en otras iglesias y basílicas (aquí se puede leer sobre esto un magnífico artículo de Francisco Martín Casalderrey en Suma).

Civita Castellana – Santa Maria Maggiore

El triángulo de Sierpinski es un ejemplo de fractal, objetos matemáticos que se pueden definir por poseer la propiedad de autosimilaridad (si ampliamos un trozo, encontramos el mismo patrón siempre, lo que ocurre en el triángulo de Sierpinski, como vemos por su propia construcción).

Aunque el triángulo original lo vamos “consumiendo” en nuestro proceso, algo queda. Y somos capaces de saber que dimensión tiene. Para ello, se usa la llamada dimensión Hausdorff. En el caso del triángulo de Sierpinski, sospechamos que la dimensión estará entre 1 y 2, y efectivamente, su dimesnión fractal o de Hausdorff es ln 3/ln 2, aproximadamente 1,585. Así que nuestro triángulo no es tan evanescente como podría parecer.

Este cálculo se hace tomando esta definición de dimensión fractal:

Dimensión del fractal = logaritmo del número de piezas autosimilares/logaritmo del factor de magnificación

Por supuesto, existen construcciones similares y análogos en dimensiones superiores, todos ellos objetos fractales, y de una gran belleza.

Para finalizar, digamos que existe un proyecto para construir el mayor triángulo de Sierpinski del mundo, a cargo del profesor José Luis Rodríguez Blancas (el mago Moebius) de la Universidad de Almería y de su equipo; aquí se pueden encontrar detalles del mismo.

Sobre la canción de Radiohead: “How to dissapear completely” está basada en un sueño de Thom Yorke en el que veía flotando como un fantasma. “I float down the Liffey” puede referirse al río Liffely que aparece en el Ulises de James Joyce. Los versos “I’m not here, this is not happening”, se suponen una referencia al consejo que Michael Stipes, de R.E.M., le dio a Thom para enfrentar el estrés de la gira O.K. Computer.

Esta es una de las canciones mas hermosas de Radiohead, en la que música y palabras se combinan de una manera magistral, creando un ambiente onírico. Desaparecemos a cada momento, porque cada segundo que pasa ya no somos los mismos que erámos. ¡Y cuántas veces nos gustaría desaparecer por completo de verdad, aunque solo fuera por unos momentos!

Esta entrada es para Esther, confiando en que su risa no desaparezca nunca (ni tan siquiera parcialmente).

—

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU)

Compartir