Elipse: la prueba del helado

Todo matemático (o amante de las matemáticas) que se precie, conocerá la definición de elipese como lugar geométrico:
Una elipse es el lugar geométrico de los puntos del plano tales que sumadas sus distancias a dos puntos fijos, llamados focos, es igual a una constante.
Sin embargo, también hay otra definición alternativa de elipse como sección cónica
Una elipse es la intersección de un cono recto de revolución por un plano oblicuo que corta a todas las generatrices del cono. Si el plano es perpendicular al eje del cono, entonces la intersección es una circunferencia,
La pregunta es... ¿cómo sabemos que ambas definiciones coinciden? En este post lo vamos a ver y gracias a un helado.
La demostración que vamos a ver a continuación se conoce en el mundillo matemático como "Ice Cream Proof" y puede encontrarse en el clásico libro Calculus de Tom Apostol.
Pues empecemos por la segunda.
Tomemos un cono recto (en realidad medio cono y entenderé que el vértice está abajo, como si fuera el cucurucho del helado de la imagen) y cortémoslo por un plano (oblicuo, no recto) que corte a todas las generatrices. La sección de ese plano con el cono es nuestra elipse, pero.. ¿quienes serán los focos?
Para encontrarlos, hay que encontrar las esferas tangentes al cono y al plano a la vez. De hecho hay dos, una debajo del plano y otra por encima. Los focos de la elipse serán los puntos de tangencia de esas esferas con el plano.
Vamos a ver un dibujo.

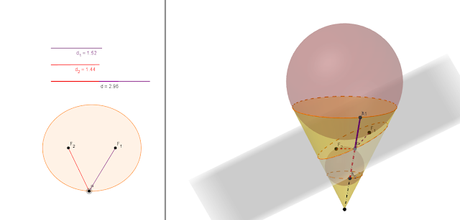
A la derecha vemos la construcción geométrica en 3D y a la izquierda tenemos lo que pasa en el plano secante. ¿Veis ya el porqué del nombre de la prueba?
Voy a poners la parte 3D un poco más grande.

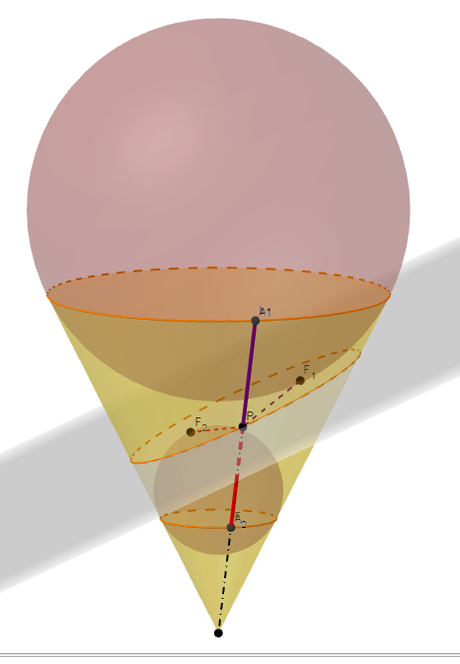
Vamos a justificar ahora que los focos definidos como puntos de tangencia, coinciden con la definición inicial de foco.
Llamemos $F_1$ al punto de tangencia de la esfera de arriba con el plano y $F_2$ al de abajo.
Tomemos un punto $P$ de la elipse y tracemos la generatriz del cono que pasa por $P$. Esta generatriz es TANGENTE a amabas esferas; llamemos $A_1$ y $A_2$ a los puntos de tangencia correspondientes.
Ahora tracemos los segmentos que van desde $P$ hasta $F_1$ y $F_2$. El segmento $\overline{PF_1}$ es tangente a la esfera de arriba en $F_1$, pero el segmento $\overline{PA_1}$ es también tangente a la esfera (esta vez en $A_1$). Entonces es claro que ambos segmentos tienen LA MISMA LONGITUD.
Análogamente, los segmentos $\overline{PF_2}$ y $ \overline{PA_2}$ tienen la misma longitud.
Pero como resulta que $A_1$, $A_2$ y $P$ están alineados, tenemos que $d(P,A_1)+d(P^,A_2)=d(A_1,A_2)$. Así que reuniendo todo tenemos que
$$d(P,F_1)+d(P,F_2)=d(P,A_1)+d(P,A_2)=d(A_1,A_2)$$
y este último número $d(A_1,A_2)$ es INDEPENDIENTE de $P$, es decir, es CONSTANTE.
por lo tanto hemos demostrado que fijado cualquier punto $P$ de la elipse, la suma de las distancias a dos puntos fijos $F_1$ y $F_2$ es igual a una constante. Y esta, queridos amigos, es la definición originale de elipse como lugar geométrico.
Ahora os voy a poner el applet de Geogebra para que jugueteéis un poco con él y vayáis cambiando cosillas.

Acceso directo a Ice Cream Proof: elipse.
Se pueden hacer pruebas similares para las otreas cónicas, hipérbolas y parábolas, pero eso lo dejo ya para otro post que espero publicar en breve. Atentos a la pantalla.
Tito Eliatron Dixit
PD: Esta entrada participa en la Edición 1 del Año X del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.  
 
Esta entrada se ha publicado originalmente en Tito Eliatron Dixit.
Si la estás viendo en otra web, probablemente estés siendo víctima de un engaño.
 
SI no ves las fórmulas correctamente, entra en Tito Eliatron Dixit, donde sí podrás verlas.