Para el primero de los métodos vamos a utilizar la definición pura y dura de la circunferencia: el lugar geométrico de los puntos del plano que equidistan del centro.
Así, elegimos 2 puntos
 y
y  de la circunferencia y trazamos el segmento que los une.
de la circunferencia y trazamos el segmento que los une. Seguidamente, con un compás, haciendo centro en
Seguidamente, con un compás, haciendo centro en  , trazo arcos de circunferencias con radio algo mayor que la mitad del segmento; y lo mismo, haciendo centro en
, trazo arcos de circunferencias con radio algo mayor que la mitad del segmento; y lo mismo, haciendo centro en  (y con el mismo radio). Los dos puntos de corte definen la mediatriz
(y con el mismo radio). Los dos puntos de corte definen la mediatriz  del segmento
del segmento  , es decir, la recta formada por todos los puntos que están a la misma distancia de ambos.
, es decir, la recta formada por todos los puntos que están a la misma distancia de ambos. Ahora tomamos un tercer punto
Ahora tomamos un tercer punto  , trazamos el segmento
, trazamos el segmento  y calculamos la mediatriz
y calculamos la mediatriz  de este segmento por el mismo procedimiento anterior.
de este segmento por el mismo procedimiento anterior.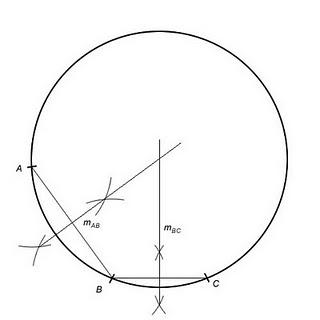
Entonces el punto de corte de ambas mediatrices, es decir,
 será el centro de la circunferencia.
será el centro de la circunferencia. En efecto, este punto está a la misma distancia de
En efecto, este punto está a la misma distancia de  ,
,  y
y  y, además, es el único (pues dos rectas que se cortan lo hacen en un único punto. Por lo tanto, ese punto ha de ser el centro de la circunferencia en la que están contenidos.
y, además, es el único (pues dos rectas que se cortan lo hacen en un único punto. Por lo tanto, ese punto ha de ser el centro de la circunferencia en la que están contenidos.Además, como corolario de esta construcción, se deduce que por 3 puntos no alineados pasa una única circunferncia.
Bien, este método es el clásico, en el sentido que sólo se precisan como aparejos de cálculo una regla (para trazar rectas) y un compás (para trazar circunferencias de centro y radio dados). Sin embargo, vamos a ofrecer otro método que sólo precisa de una única herramienta y que, además, hace uso de una curiosa propiedad de las circunferencias.
La herramienta que vamos a usar es una escuadra (o un cartabón, que eso va a dar igual). En realidad, basta utilizar un simple ángulo recto.
En primer lugar, partimos de un punto
 de la circunferencia y ponemos el vértice del ángulo recto de la escuadra sobre él (realmente, da igual la inclinación), lo importante es que los lados del ángulo recto corten a nuestra circunferencia.
de la circunferencia y ponemos el vértice del ángulo recto de la escuadra sobre él (realmente, da igual la inclinación), lo importante es que los lados del ángulo recto corten a nuestra circunferencia.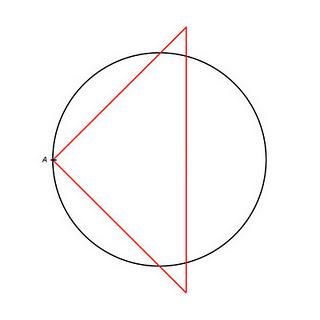
Seguidamente, nos fijamos en los puntos de corte de los lados que forman el ángulo recto con la circunferencia y les ponemos nombre:
 y
y  .
. Ahora elijo otro punto de la circunferencia
Ahora elijo otro punto de la circunferencia  y repito el proceso anterior, llamando ahora
y repito el proceso anterior, llamando ahora  y
y  a los puntos de corte
a los puntos de corte Ahora si trazamos los segmentos
Ahora si trazamos los segmentos  y
y  , éstos se cortarán en un punto $$O$$. Ese punto es el centro de la circunferencia.
, éstos se cortarán en un punto $$O$$. Ese punto es el centro de la circunferencia. Vale, Tito, ese es el centro... porque tú lo dices, ¿no? Pues no, no lo digo yo, sino una propiedad que es el Arco Capaz. Si tenemos un ángulo inscrito en la circunferencia (es decir, un ángulo cuyo vértice está en la circunferencia), éste la cortará en dos puntos; si ahora trazamos el ángulo que tiene como vértice el centro de la circunferencia y pasa por los dos puntos anteriores, la medida de este ángulo es el doble que el original. Mejor míralo en este dibujo:
Vale, Tito, ese es el centro... porque tú lo dices, ¿no? Pues no, no lo digo yo, sino una propiedad que es el Arco Capaz. Si tenemos un ángulo inscrito en la circunferencia (es decir, un ángulo cuyo vértice está en la circunferencia), éste la cortará en dos puntos; si ahora trazamos el ángulo que tiene como vértice el centro de la circunferencia y pasa por los dos puntos anteriores, la medida de este ángulo es el doble que el original. Mejor míralo en este dibujo: Bueno, pues ¿qué hemos hecho nosotros? trazar ángulos inscritos de 90º, con lo que los cortes con la circunferencia definen un ángulo de 180º. Total, que los segmentos
Bueno, pues ¿qué hemos hecho nosotros? trazar ángulos inscritos de 90º, con lo que los cortes con la circunferencia definen un ángulo de 180º. Total, que los segmentos  y
y  son, en realidad, diámetros de la circunferencia. Y es, entonces, obvio que la intersección de dos diámetros es el centro de nuestra circunferencia.
son, en realidad, diámetros de la circunferencia. Y es, entonces, obvio que la intersección de dos diámetros es el centro de nuestra circunferencia.Para finalizar, si algún día vais a un bar (ejem) y os encontráis con un posavasos, de esos de papel, circular. ¿Cómo calcularías su centro? Claro, ahora no tienes nada a mano (no, chicas, el pintalabios no vale en este caso; no, el pintalabios de tu novia, tampoco ¬¬). Así que tendremos que utilizar otro método. Por ejemplo, puedes tratar de doblar (a ojo) el posavasos de forma que obtengas medio círculo. Entonces el doblez será un diámetro. Si repites el proceso, pero doblando en otra dirección, construyes un segundo diámetro y el punto donde ambos dobleces se encuentren será, más o menos, el centro de tu posavasos.
Hala, ya tienes de qué hablar en un bar.
Por cierto, ya que estamos, os querría pedir un favor. ¿Se os ocurren algunas otras construcciones, esencialmente diferentes a las aquí explicadas, para obtener el centro de una circunferencia dada? ¿Y para hallar el centro del posavasos?
Tito Eliatron Dixit
Si te ha gustado esta entrada, puedes dejar un comentario directamente en Tito Eliatron Dixit.
O votarme en los premios Bitacoras 2011:


