Encuentra soluciones buscando triángulos. El teorema de Tales

En la mayoría de ocasiones para encontrar la solución a un problema, primero tenemos que buscar datos relevantes.Cómo un buen detective!                                                                                                                 En geometría, ante cualquier situación planteada es importante buscar aquellos elementos que nos interesen.

Dos hechos históricos

Se cuenta que el matemático Tales de Mileto (siglo VI a.C.), utilizando la semejanza de triángulos y su ingenio resolvió dos problemas nada sencillos en su época.

                                                          ¿A qué distancia estaban los barcos enemigos?

                                                         ¿Qué altura tenía  la gran pirámide de Keops?

Antes de ver cómo pudo encontrar la solución el gran sabio griego, ¿te atreves a plantear el problema haciendo un pequeño esquema?

Para facilitarte las cosas, te muestro sobre la pantalla algunas cosas que te vendrá bien recordar.

Semejanza de triángulos

Ten en cuenta que dos triángulos son semejantes si tienen sus ángulos correspondientes iguales y si sus lados homólogos son proporcionales entre sí.

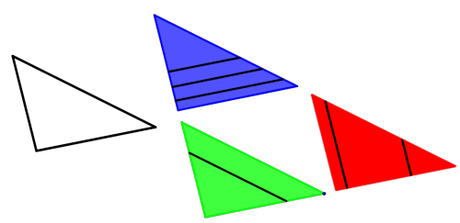
Triángulos semejantes trazando paralelas

También es importante que recuerdes que si en un triángulo trazas una línea paralela a cualquiera de sus lados, obtendrás dos triángulos semejantes. Mira cuantos sale ahora! Por ejemplo, en el polígono azul hay 4 triángulos semejantes.

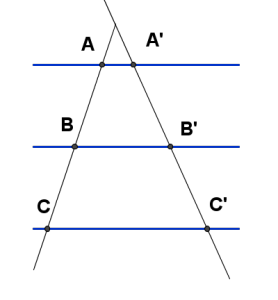
Teorema de Tales sobre triángulos semejantes 

¿Te acuerdas? Afirma que si dos rectas cualesquiera se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.

Dicho de otra forma.Cuando veas rectas paralelas,”córtalas” y obtendrás varias razones de semejanza.

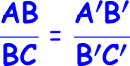
El teorema de Tales y las catapultas

Cuando la ciudad de Mileto, situada en la costa griega, iba a ser atacada por los barcos enemigos, los soldados recurrieron a Tales. Necesitaban saber a que distancia se encontraba una nave para ajustar el tiro de sus catapultas.

El genio matemático resolvió el problema sacando una vara por la cornisa del acantilado, de tal forma que su extremo coincidiera con la visual del barco. Conociendo su altura (h), la del acantilado (a) y la longitud de la vara (v), calculó sin dificultad la distancia deseada (x). Parece sencillo, ¿verdad?

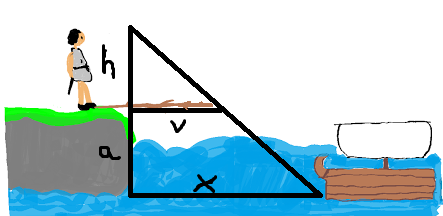
Observa que ahora tenemos dos triángulos semejantes, de tal forma que al ser sus lados proporcionales, podemos establecer la siguiente igualdad.

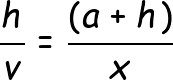
De esta forma consiguió calcular el valor de la distancia x. El resto de datos ya los conocía.

Calculó la altura de la gran pirámide egipcia 

Según narra Herodoto, Tales calculó la altura de la gran pirámide de Keops, situada en Guiza, la más antigua de las siete maravillas del mundo.

¿Cómo lo hizo?  Usando su teorema, el gran sabio pensó que en el momento que su sombra midiese lo mismo que él, los rayos del Sol formarían un grado de 45 grados con la cima de la pirámide y con su cabeza. Y por tanto, en ese preciso instante la altura de la pirámide sería igual a la sombra de la misma.

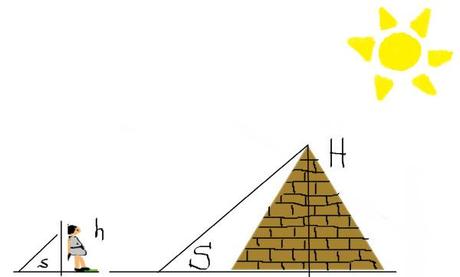
Observando el dibujo, podemos llamar h a la altura de Tales y s a su sombra.

En el momento que  s=h, los rayos del Sol formaran un ángulo de 45 grados en la cabeza de Tales y con la cima de la pirámide (al ser los rayos del Sol paralelos entre sí). Por tanto, en ese mismo momento H=S.

Como estamos mirando triángulos semejantes, midiendo la sombra de la pirámide (S), conoceremos su altura (H), que será la misma.

Observa que se trata de triángulos semejantes, porque sus ángulos homólogos son iguales. Los dos triángulos dibujados tienen un ángulo recto y dos ángulos de 45 grados.

Datos curiosos sobre Tales de Mileto

Nuestro personaje de hoy, fue un célebre astrónomo, filósofo y matemático griego. Es considerado como uno de los siete sabios de Grecia. Vivió en la misma época que Pitágoras.Parece que fue el primero en explicar la razón de los eclipses de sol y de luna. Descubrió varias proposiciones geométricas. Cuentan los historiadores que murió asfixiado por la multitud, cuando se retiraba de un espectáculo.

Este es uno de los episodios anecdóticos atribuidos a Tales: Cierta noche paseaba el matemático completamente absorto mientras contemplaba las estrellas y, por al no prestar suficiente atención al terreno que pisaba, cayó  dentro de un gran hoyo. Una vieja, que pasaba por allí vio el accidente y le dijo, “¿cómo quieres ¡oh sabio! saber lo que pasa en el cielo si no eres capaz de saber lo que ocurre en tus pies?”

Destacó gracias a su sabiduría práctica, a su notable capacidad política y a la gran cantidad de conocimientos que poseía. Se le atribuye la máxima “En la confianza está el peligro”.

Utiliza las sombras para medir ciertas longitudes inaccesibles

Ahora te toca a tí. A continuación de te dejo sobre la pantalla dos problemas para aplicar el teorema de Tales. Si tienes ganas, puedes probar a solucionarlos. Tienen su utilidad.

♣ Calcula la altura de un edificio sabiendo que en un determinado momento del día proyecta una sombra de 6 metros, y una persona que mide 1,8 m. tiene, en ese mismo instante, una sombra de 70 cm.

¿Y si está nublado?

No importa, siempre puedes encontrar alguna referencia que te sirva.

♠ María quiere conocer la altura de la torre de la Giralda en Sevilla. Cuando sale a la calle se separa de la base de la torre 8,5 m y observa que para ver el extremo superior necesita un ángulo de elevación respecto a la horizontal de aproximadamente 85°. Si María mide 1,70 m, ¿cuál es la altura aproximada de la Giralda?

¿Te ha parecido interesante? Agradezco tus comentarios. Puedes compartir en tus redes sociales.

Ilustraciones de Lucía Fernández          Fuentes 1 2