'Entidad límite: La Armada Deidilio'

El post de hoy va a ser un poco especial, ya que además de mencionar ejemplos de buena ciencia, hablaré sobre una novela cuyo autor, Marcos Quijada, me consultó en su día por algunas cosillas mientras la escribía, y ha tenido el detalle de mencionarme en los agradecimientos. Se trata de «Entidad Límite: La Armada Deidilio». No la encontraréis en ninguna librería, ya que sólo está disponible a la venta online, en Amazon (en papel o en formato e-book) y en Lulu.

Es una historia de ciencia ficción ambientada en el presente, pero en la que una pequeña parte de la humanidad lleva habitando colonias espaciales en secreto, desde hace algunos miles de años, gracias a la ayuda de alienígenas. Existe algo llamado «universo etéreo» que sirve al doble propósito de permitir el viaje y la comunicación más rápido que la luz, y de proporcionar posibles explicaciones racionales a la existencia de espíritus, del alma, o incluso de Dios. Tal vez alguno piense que esto último raya el esoterismo, pero cuando la acción se limita al «universo físico» (el universo real que todos conocemos, o intentamos conocer), la física es muy rigurosa, acercándose mucho a la ciencia ficción hard, y conteniendo bastantes ejemplos de buena ciencia.

Así, se nos narra un viaje a y desde la Luna (donde hay una base oculta), en el que una nave espacial recorre la mitad del camino con una aceleración constante de 4 g (4 veces la aceleración de la gravedad terrestre), que los pasajeros deben sufrir con incomodidad. Luego detiene su aceleración mientras da la vuelta , momento en el que los pasajeros experimentan ingravidez, y finalmente decelera el resto del camino a 4 g (similar a lo que vemos en el álbum de Tintín Aterrizaje en la Luna). Se indica además que la duración de cada tramo es de 50 minutos, lo cual encaja si hacemos los cálculos necesarios: el radio medio de la órbita lunar es de 384.400 km, y aplicando la conocida fórmula e=1/2·a·t² para calcular la distancia recorrida en un movimiento uniformemente acelerado en cada tramo (recordando que 1 g son 9,8 m/s²), salen unos 352.800 km. Algo menor que la distancia Tierra-Luna, pero la nave no inicia ni termina el viaje a 4 g en la superficie de ambas, sino a una cierta distancia.

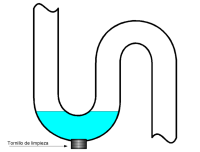
Otro ejemplo de buena ciencia, y además, con un diseño ingenioso, es el sistema de esclusas de la base lunar. Esta base se encuentra bajo tierra, y la comunicación con la superficie se hace mediante un simple conducto en forma de «U» parcialmente relleno de agua, similar a los que se usan en los desagues. Para los no muy duchos en fontanería, la tubería que desciende del desague de un lavabo, inodoro o bañera, tiene forma de «S» tumbada. El tramo de «U» invertida actua como sifón, permitiendo que el agua suba para bajar después. Pero lo interesante es la parte en forma de «U», donde siempre queda algo de agua, taponando ese codo, y evitando que el aire del interior de la instalación salga al exterior, arrastrando malos olores. Por el principio de vasos comunicantes, la altura que alcanza el agua es el mismo en ambos lados de la U. Pero si en uno de los lados la presión del aire fuera mayor que en el otro, en el lado de menor presión la altura del agua sería mayor, de forma que la diferencia de peso entre las columnas de agua compense la diferencia de presiones en ambos lados (la presión de una columna de líquido es igual a su peso dividido entre la superficie de su base), pudiendo llegar al extremo en el que en uno de los lados, no haya presión atmosférica en absoluto, de forma que la columna de líquido por sí sola proporciona toda la presión necesaria, como en el barómetro de Torricelli.

Así, la base lunar se comunica con la superficie mediante este sistema. En el lado de la base, el extremo de la U termina en un lago artificial, y la altura del agua en el otro extremo es tal que iguala la presión producida por el aire de la base. Las naves simplemente se sumergen por un extremo, recorren el conducto, y emergen por el otro, sin necesidad de esclusas. ¿Y no se evapora el agua? Bueno, como sabéis, en el vacío el agua no puede permanecer líquida. Para solucionar ese problema, el autor recurre a un líquido ficticio en el último tramo del lado de la superficie lunar, menos denso que el agua para que flote sobre esta, pero con unas propiedades que le permiten permanecer líquido en las condiciones de temperatura y presión lunares.

Las cifras también cuadran aquí. La presión atmosférica en la Tierra equivale a la de una columna de agua de 10 m. En la novela, la base lunar tiene dos atmósferas de presión, lo que equivaldría a una columna de 20 m de altura. Pero la gravedad lunar es aproximadamente 1/6 de la terrestre, por lo que necesitamos 6 veces más masa para tener la misma presión, es decir, la altura de la columna de agua debe ser 6 veces mayor. Eso nos da 120 m de altura, que es la cifra que se menciona en la novela.

Hay otro detalle que me encanta. Las estaciones espaciales son cilindros de O'Neill, que generan pseudogravedad mediante rotación (como en Babylon 5). Uno de los protagonistas pregunta cuánta energía hace falta para mantenener el giro de tan enormes estructuras, y la respuesta que recibe es: «cero». Efectivamente, una vez tienes un objeto en rotación flotando en el vacío, si no se ejercen fuerzas sobre él, la velocidad de rotación se mantiene. Es lo que se conoce como conservación del momento angular, y es el motivo de que los planetas sigan rotando desde su formación. Como curiosidad, un personaje menciona que en alguna ocasión hubo que reajustar la velocidad de giro, ya que el trasiego de naves entrando y saliendo, alteraba el momento angular, hasta que definieron unos protocolos concretos de atraque y desatraque para compensar unos y otros (estas entradas y salidas se realizan por el eje, y utilizan el mismo sistema de «esclusa fontanera» que en la base lunar). Aunque no se menciona, también habría otras pequeñas variaciones de momento angular inevitables, debidas al propio movimiento de masas en la estación (gente y objetos desplazándose y cambiando de lugar).

Me estoy extendiendo mucho, así que terminaré con otro detalle, donde puede haber algo de mala ciencia (deliberada, pues Marcos ya era consciente del problema cuando me lo planteó). Parte de la acción transcurre en un satélite habitado de un planeta gigante gaseoso, que se ve bastante grande en el cielo. A lo largo de su órbita, hay momentos en los que el satélite está entre el planeta y la estrella, de forma que por las noches recibe la luz reflejada del planeta (como nuestra luna llena, pero a lo bestia) haciéndolas bastante luminosas. Y al contrario, hay veces en las que el satélite está «detrás» del planeta, de forma que éste eclipsa la estrella durante dos semanas, produciendo una estación de noche constante, en la que las temperaturas globales bajan mucho. El problema es que esa duración no es posible. Para que el eclipse dure tanto tiempo, parece lógico pensar que el planeta debe verse muy grande desde el satélite. Eso quiere decir que el satélite está cerca del planeta. Pero cuanto más cercano al planeta, el periodo orbital es mucho menor, es decir, el satélite se mueve más deprisa.

Vamos a ver algunos ejemplos con datos reales con Júpiter y sus satélites. Para no complicar demasiado el texto, el detalle de los cálculos que he utilizado está al final del post, y así los que tengan interés lo podrán revisar (si hay errores, decídmelo, por favor). Veamos los cálculos para algunos satélites.

SatéliteDistancia aproxPeriodo orbitalDuración eclipse

Io 421.700 km 1,8 días 2,3 horas

Calisto 1.882.709 km 16,7 días 4,8 horas

Leda 11.097.250 km 238,8 días 11,8 horas

Megaclite 24.687.260 km 792 días 17 horas

Como veis, Io y Calisto están demasiado cerca como para tener estaciones de semanas o meses. Los otros dos, ya tienen una duración de «año» de cientos de días, pero el eclipse dura menos de un día. Cuanto más lejos esté el satélite, más largo es el eclipse, pero también más duración tiene el periodo orbital, y más pequeño se ve el planeta.

Si el planeta de la novela fuera más grande y menos masivo que Júpiter (por tanto, menos denso), tal vez se podría encontrar unas proporciones en las que el periodo orbital sea de varios meses, y el eclipse dure dos semanas. Saturno, por ejemplo, es menos denso que Júpiter (e incluso que el agua). Existe un planeta extrasolar denominado HAT-P-1b cuya densidad es unas tres veces menor que la de Saturno, siendo el planeta menos denso conocido. Y aún así, su diámetro es poco mayor que el de Júpiter y su masa es la mitad de la de éste, lo que supondría multiplicar por dos los periodos orbitales y duraciones de eclipses que hemos visto para los satélites jovianos. Como veis, tampoco es suficiente. Y hay un límite inferior para la densidad de un planeta. Es la propia gravedad del planeta la que lo mantiene «unido». Los gigantes gaseosos están compuestos sobre todo por hidrógeno y helio, que son los elementos más ligeros. Si la masa (y por tanto la gravedad) no fuera suficientemente elevada, gases tan ligeros escaparían poco a poco al espacio. ¿Cuál es ese mínimo? Bueno, francamente, no lo sé.

Nota: Para calcular la duración de un eclipse de sol desde un satélite de Júpiter, he simplificado la realidad, suponiendo que las órbitas de los mismos son circulares y coinciden con el plano de la órbita de Júpiter. Además, he considerado que el eclipse dura mientras el satélite esté en el arco de circunferencia correspondiente a una cuerda de longitud igual del diámetro de Júpiter. La realidad es diferente, pero creo que el resultado es más o menos aproximado (lo que interesa es tener una idea del orden de magnitud). He calculado el ángulo recorrido durante el eclipse, a partir de la longitud de la cuerda y el radio de la órbita, con la fórmula 2·arcsen(c/2R), donde c es la longitud de la cuerda, y R el radio de la circunferencia.