
La semana pasada vimos cómo se podía usar la estrategia Epsilon-Greedy para resolver un problema tipo bandido multibrazo. Una estrategia que nos había dado mejores resultados que un test A/B. Pero esta estrategia tiene un problema, una vez que se sabe cuál es el mejor bandido se continuará jugando una cantidad de veces con bandidos que no son el óptimo. Lo que se puede resolver utilizando una estrategia Epsilon-Greedy con decaimiento. Esto es, cambiando la probabilidad con la que se juega con bandidos aleatorios a medida que aumenta el conocimiento del agente del entorno.
La estrategia Epsilon-Greedy con decaimiento
Uno de los problemas de la estrategia Epsilon-Greedy es que independientemente del número de episodios continúa explorando con todos los bandidos el mismo porcentaje de veces. Algo que no es necesario cuando se conoce cuál es el bandido óptimo. La solución de este problema es sencilla, simplemente reducir el valor de épsilon, el porcentaje de veces que se juega aleatoriamente, a medida que aumenta el número de episodios. De este modo, en los primeros episodios, cuando se desconoce la recompensa esperada, se juega aleatoriamente y, a medida que se tiene más información, se juega de manera óptima.
Decaimiento del parámetro épsilon
Se pueden usar diferentes estrategias para obtener un valor de épsilon que decaiga con el tiempo. Ya que solamente es necesario que este decaiga a medida que aumente el número de episodios. Por lo que una de las formas más sencillas sería usar un valor inversamente proporcional al número de episodios, resto es, 1/N donde N es el número de episodios.
Otra opción, la que se va a implementar a continuación, es comenzar con un valor de épsilon dado y reducir el valor de este multiplicándose en cada episodio por un factor que sea menor inferior a la unidad. Así, el valor en cada tirada sería epsilon * decay^N donde, al igual que antes, N es el número de episodios.
Implementación de Epsilon-Greedy con decaimiento en Python
Para implementar el método de Epsilon-Greedy se van a crear dos clases. Una clase Bandit en la que se implementa un bandido con una recompensa que se genera mediante una distribución binomial. Por otro lado, la clase Epsilon en la que se implementa el agente. Código que se muestra a continuación.
import numpy as np
import matplotlib.pyplot as plt
class Bandit:
"""
Implementación de un Bandido Multibrazo (Multi-Armed Bandit) basado
en una distribución binomial
Parámetros
----------
number: integer
Número de recompensas que puede devolver el agente
probability : float
Probabilidad de que el objeto devuelva una recompensa
Métodos
-------
pull :
Realiza una tirada en el bandido
"""
def __init__(self, probability, number=1):
self.number = number
self.probability = probability
self.reward = self.number * self.probability
def pull(self):
return np.random.binomial(self.number, self.probability)
class Epsilon:
"""
Agente que soluciona el problema del el Bandido Multibrazo
(Multi-Armed Bandit) mediante el uso de una estrategia Epsilon
Greedy
Parámetros
----------
bandits : array of Bandit
Vector con los bandidos con los que se debe jugar
epsilon : float
Porcentaje de veces en las que el agente jugada de forma
aleatoria
decay : float
Velocidad con la que decae la probabilidad de seleccionar una
jugada al azar
Métodos
-------
run :
Realiza una tirada en el bandido
average_reward :
Obtención de la recompensa promedio
plot :
Representación gráfica del histórico de jugadas
reset :
Reinicia el agente
"""
def __init__(self, bandits, epsilon=0.05, decay=1):
self.bandits = bandits
self.epsilon = epsilon
self.decay = decay
self.reset()
def run(self, episodes=1):
for i in range(episodes):
prob = np.random.random()
# Selección entre la jugada aleatoria o avariciosa
if prob < self._epsilon:
bandit = np.random.choice(len(bandits))
else:
max_bandits = np.where(self._mean == np.max(self._mean))[0]
bandit = np.random.choice(max_bandits)
# Decaimiento del parámetro epsilon
self._epsilon *= self.decay
# Obtención de una nueva recompensa
reward = bandits[bandit].pull()
# Agregación de la recompensa al listado
self._rewards.append(reward)
# Actualización de la media
self._plays[bandit] += 1
self._mean[bandit] = (1 - 1.0/self._plays[bandit]) * self._mean[bandit] \
+ 1.0/self._plays[bandit] * reward
return self.average_reward()
def average_reward(self):
return np.mean(self._rewards)
def plot(self, log=False, reference=False, label=None):
cumulative_average = np.cumsum(self._rewards) / (np.arange(len(self._rewards)) + 1)
if label is None:
plt.plot(range(len(self._rewards)), cumulative_average)
else:
plt.plot(range(len(self._rewards)), cumulative_average, label=label)
if reference:
for reward in [b.reward for b in self.bandits]:
plt.plot([0, len(self._rewards)], [reward, reward],
label=f'reward={reward}')
if log:
plt.xscale('log')
def reset(self):
self._epsilon = self.epsilon
self._rewards = []
self._plays = [0] * len(self.bandits)
self._mean = [0] * len(self.bandits)
La clase Bandit
En la clase Bandit existen dos propiedades: number que indica la recompensa máxima que se puede obtener en una tirada, valor que por defecto es igual a la unidad, y probability la probabilidad de éxito. Además de esto se calcula la recompensa promedio esperada, lo que para una distribución binomial es el producto de los dos parámetros.
Solamente se ha implementado un método, pull(), a través del cual se obtiene el resultado de una tirada.
La clase es una simplificación de la que usamos en entradas anteriores, ya que no guarda las recompensas históricas ni el promedio de estas. Lo que se ha implementado en esta ocasión dentro de la clase Epsilon
La clase Epsilon
El código de la clase Epsilon es más compleja, ya que incluye la lógica del agente. Una clase que cuenta con tres parámetros: bandits un vector con el listado de bandidos, epsilon la probabilidad con la que jugará al azar el agente y decay el parámetro con el que decae el valor epsilon. Por otro lado, la clase cuenta con cuatro métodos run(), average_reward(), plot() y reset()
El método run() jugará el número de episodios indicadas con los bandidos. En primer lugar, calculará un valor al azar y si este es menor que el valor de épsilon lo hará al azar, mientras que en el resto de los casos seleccionará el mejor agente. Al igual que se hizo para el caso de Epsilon-Greedy, en el caso de una recompensa promedio se seleccionará el bandido al azar. Posteriormente, se jugará con el bandido y se calculará el nuevo valor de épsilon, se agregará la recompensa al histórico y se actualizará la recompensa promedio para cada bandido. Devolviendo como resultado la recompensa promedio.
Algo que se puede ver en el código es que si el valor de decay es igual a la unidad, valor por defecto, entonces la clase implementa el método Epsilon-Greedy normal. Para implementar Epsilon-Greedy con decaimiento es necesario que decay sea un valor menor que 1 y positivo.
average_reward()
El método average_reward() simplemente calcula la recompensa promedio para el agente.
El método plot() permite representar la recompensa media acumulada para ver cómo evoluciona esta con el tiempo. Gráfica a la que se puede añadir la recompensa promedio que se esperaría para cada agente. Opcionalmente también se puede cambiar el eje de coordenadas x para que se emplee escala logarítmica, algo que es de gran utilidad cuando el número de episodios es elevado.
Finalmente, el método reset() permite reiniciar el agente. Algo que se puede utilizar si se desea volver a jugar con los mismos bandidos desde el principio.
Resultados
Ahora se puede comparar los resultados que se obtienen para 10.000 episodios con Epsilon-Greedy y Epsilon-Greedy con decaimiento. Para lo que solamente se tendría que usar el siguiente código.
np.random.seed(0) bandits = [Bandit(0.02), Bandit(0.06), Bandit(0.10)] epsilon = Epsilon(bandits) decay = Epsilon(bandits, epsilon=1, decay=0.999) epsilon.run(10000) decay.run(10000)
Lo primero que se puede ver es que el método sin decaimiento tiene una recompensa de 0,093, mientras el método con decaimiento de 0,094. Una ligera mejora para el segundo, pero que todavía no es significativa.
El valor que se debería esperar para el método sin decaimiento es de 0,098. Esto es 95% por la recompensa del mejor bandido más 5% por la recompensa promedio de todos los bandidos. Esto es: 0,95 * 0,1 + 0,05 * (0,18/3) lo que da 0,098.
Por otro lado, a medida que aumenta el número de episodios el valor de Epsilon-Greedy con decaimiento debe acercarse al del mejor bandido. Ya que, el valor de épsilon tenderá a cero, por lo que solamente jugará con este.
Esto es algo que se puede comprobar aumentando el número de episodios. Por ejemplo, con un millón de episodios más los valores pasarán a ser de 0,0985 y 0.0998 para Epsilon-Greedy y Epsilon-Greedy con decaimiento respectivamente. Valores ya muy cercanos a los que se esperaría para ambos agentes.
La evolución de los 1,1 millón de episodios se puede ver en la siguiente gráfica. En donde se puede ver que ambas estrategias se acercan al valor óptimo a partir de los 10.000 episodios.
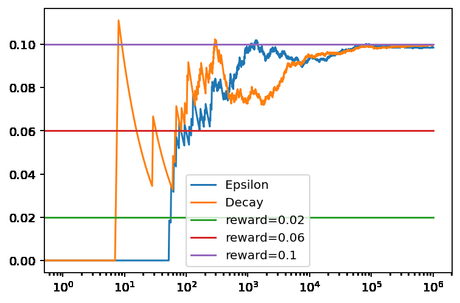
Conclusiones
La estrategia Epsilon-Greedy con decaimiento ofrece ciertas ventajas respecto a Epsilon-Greedy, especialmente cuando el número de episodios aumenta. Al seleccionar el bandido inicialmente al azar y, a medida que avanzan los episodios, cada vez de una forma más avariciosa permite obtener mayores recompensas. Ya que una vez que se conoce cual es el mejor bandido ya no es necesario explorar en busca del mejor.
