La última edición del premio Oswald Veblen de Geometría ha reconocido el trabajo conjunto del brasileño Fernando Codá Marques (Princeton University) y el portugués André Neves (Imperial College London). El jurado ha destacado su demostración de la Conjetura de Willmore, “una cuestión fundamental sobre las propiedades de las superficies curvas en el espacio euclidiano tridimensional”. Francisco Torres, investigador predoctoral del ICMAT, explica la conjetura y su reciente resolución.

El matemático Oswald Veblen da nombre al galardón mas importante en el campo de la geometría
El prestigioso premio Veblen de Geometría, creado en 1961 en memoria del matemático estadounidense Oswald Veblen, es otorgado cada tres años por la Sociedad Americana de Matemáticas (AMS). Los galardonados en la edición de 2016 son el matemático brasileño Fernando Codá Marques y el portugués André Neves: el comité destaca su extraordinario trabajo en el área de la geometría diferencial, y en especial su demostración de la célebre conjetura de Willmore [1].
El trabajo de Marques y Neves da respuesta a una cuestión fundamental sobre las propiedades de las superficies curvas en el espacio euclidiano tridimensional, que intrigaba a los geómetras desde que el matemático Thomas Willmore la enunciara en 1965.
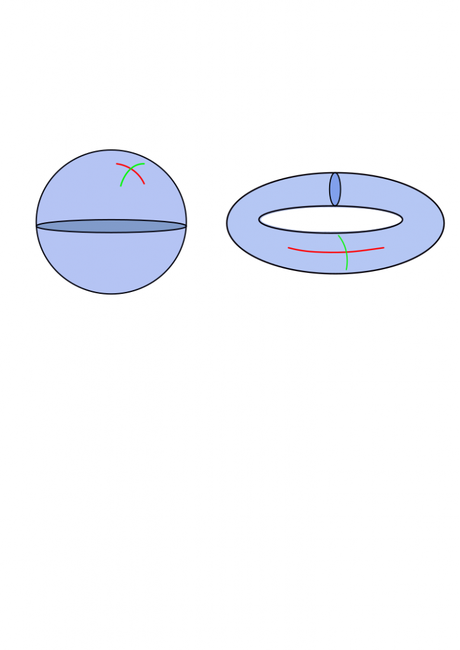
Figura 1. Esfera y toro.
A cada superficie cerrada y sin borde (por ejemplo, la superficie de un flotador o de una esfera) se le puede asociar una magnitud, la llamada energía de Willmore, que nos da una idea de cómo de curva es la superficie y, además, de hasta qué punto la curvatura en distintas direcciones trazadas sobre ella es desigual.
Volviendo al caso de la esfera, en cualquier punto de su superficie, se comba de la misma manera en todas direcciones. No ocurre así con la superficie del flotador (lo que los matemáticos llamamos toro): la curvatura de la línea verde (en la imagen 1) es mayor que la de la roja. Con algunas consideraciones adicionales, esto se acaba por manifestar en el hecho de que la esfera es la superficie con la menor energía de Willmore posible.
Como muchos otros conceptos matemáticos, la energía de Willmore no es una excepción al llamado principio de Arnold: ninguna noción matemática lleva el nombre de su auténtico descubridor (el principio de Arnold tampoco). Esta magnitud ya había sido considerada a principios del siglo XIX por los matemáticos franceses Sophie Germain y Simon Denis Poisson, como medida de la energía elástica almacenada en una superficie curvada. Aparece también en otros campos de la física, como la Relatividad General e incluso en la biología celular: las formas que adoptan algunas vesículas (los glóbulos rojos, por ejemplo) parecen deberse a que tratan de minimizar la energía de Willmore asociada a sus membranas.
La conjetura de Willmore
Willmore quería entender el comportamiento de esta energía según el tipo de superficie. Primero habrá que pensar cuántos tipos fundamentales de superficies diferentes existen. Diremos que dos superficies pertenecen a la misma especie si podemos deformar una en la otra sin rasgarla, como si fuese perfectamente moldeable. De esta manera, las superficies cerradas, orientables y sin borde se clasifican según su género, o número de agujeros:
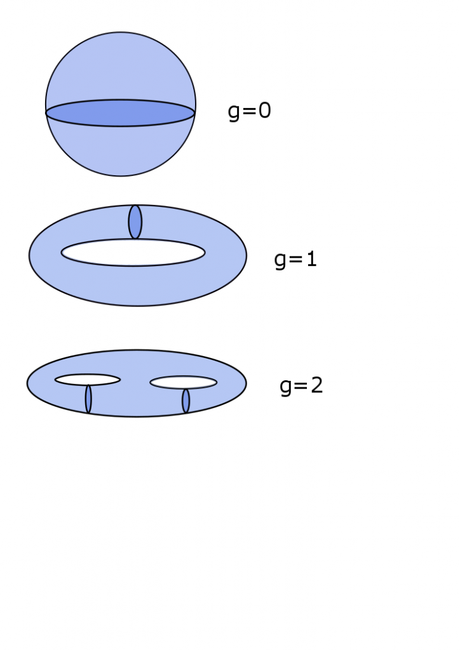
Figura 2. Géneros.
La superficie de la esfera tiene género 0, así como la de cualquier otra superficie que podamos obtener deformándola; las superficies con forma de neumático (lo que los matemáticos llaman un toro) tienen género 1.
Ya sabemos que de entre todas las superficies posibles es la esfera la que minimiza la energía. Willmore se preguntó entonces qué ocurriría si se circunscribía a las superficies de género 1, los toros, y conjeturó que, de entre todas las formas que un toro pudiese adoptar (incluyendo aquellas en las que se autointersecaba), aquella que minimizaba la energía de Willmore era la del llamado toro de Clifford. El toro de Clifford es la superficie de revolución que se obtiene al girar una circunferencia de radio 1 cuyo centro está una distancia de √2 del eje de revolución (las unidades concretas de longitud no importan, puesto que la energía de Willmore—y esta es una de las propiedades que la hacen más interesante– es invariante frente a cambios de escala de la superficie: dilataciones y contracciones).
La pregunta de Willmore, sencilla y natural, se ha resistido a los geómetras hasta que Marques y Neves han conseguido darle respuesta afirmativa: el toro de Clifford es la superficie de género 1 (y superior) que minimiza la energía de Willmore; todas las demás tienen una energía mayor. Pero el interés de su resultado no radica solamente en la respuesta en sí: cuando preguntas tan naturales son tan de difíciles de responder suele deberse a que requieren considerar nuevas técnicas y conceptos que nos permitan comprender con mayor claridad el paisaje más amplio en que estas preguntas se encuentran. El trabajo de Codá Marques y Neves ha abierto así nuevas perspectivas en muchos otros problemas del área.
Los premiados

Fernando Codá Marques (Princeton University)
Fernando Codá Marques (São Carlos, 1979) es Investigador Titular en el Instituto de Matemática Pura y Aplicada (IMPA) de Río de Janeiro y profesor en la Universidad de Princeton. Estudió el grado y máster de Matemáticas en Brasil, en la Universidad Federal de Alagoas y en el IMPA, respectivamente. Obtuvo su doctorado en la Universidad de Cornell, con José F. Escobar como supervisor.

André Neves (Imperial College London)
André Arroja Neves (Lisboa, 1975) es profesor en el Imperial College de Londres. Obtuvo su licenciatura en Matemáticas en el Instituto Superior Técnico de Lisboa, y se doctoró en la Universidad de Stanford, con Richard Schoen como supervisor.
[1] F. C. Marques, A. Neves, Min-Max theory and the Willmore conjecture, Annals of Mathematics (2014).
Más información:
http://www.ams.org/news?news_id=2866
—-
Francisco Torres es investigador predoctoral del ICMAT.
Compartir