Fracciones compuestas… no digas que no, porque sí sabes hacerlo

Una fracción, por ejemplo:

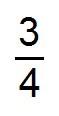
se puede entender como parte de la unidad…

… como parte de una determinada cantidad…

 … o como cociente de dos números…

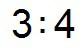
y esto es algo que se entiende sin problema.

Como también se suele aprender sin mucha dificultad como dividir dos fracciones.

Por ejemplo:

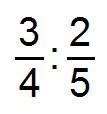
Algunas personas lo harán multiplicando la primera fracción por la inversa de la segunda…

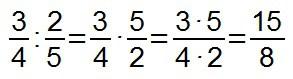
y otras, para evitar hacer el paso intermedio de la fracción inversa, directamente multiplicando sus términos “en cruz”…

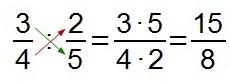
Y, como digo, esto es algo que, por lo general, se tiene más que superado.

Pero ocurre que cuando aparecen expresiones como ésta…

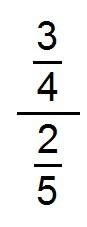
de repente todo parece complicado, el mundo se hace más grande a nuestro alrededor y nos viene un “no sé hacerlo”.

Pero… ¿Por qué?

¡Si no hay nada nuevo que no sepamos ya!

Este tipo de fracciones, a las que se llama fracciones compuestas, no son otra cosa que fracciones cuyo numerador o denominador (o los dos) contiene a su vez fracciones.

Y como tal fracción que es, se puede interpretar como cociente de dos números, que son en este caso fracciones:

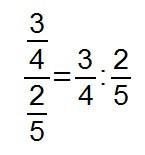
Vamos, una división de fracciones de las que sabemos hacer…

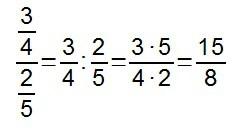
Luego, que nadie diga que no sabe hacerlo, porque sí que sabe.

Por cierto que, como suele ocurrir, tenemos también una vía más directa para hacer el cálculo de fracciones compuestas, considerando como numerador de la fracción resultado el producto de los extremos superior e inferior, y como denominador el producto de los dos valores intermedios:

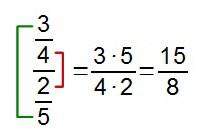
Que no es otra cosa que aprovechar que sabemos a dónde tenemos que llegar para “saltarnos” el paso intermedio de escribirlo como cociente de dos fracciones.

 Pero, como suelo decir a mis alumnos,  cada persona que lo haga como más facil le parezca y más segura esté, porque esto son matemáticas y caminos para llegar a la solución correcta hay muchos, todos igual de válidos siempre que lo que hagamos éste bien.