Las Transformaciones en el plano hacen corresponder a cada punto del plano otro punto del plano. Existen muchas formas de transformar el plano, pero hay una que es motivo de nuestro interés, esta forma consiste en transformar el plano conservando las distancias, es decir, la distancia entre dos puntos es igual a la distancia entre sus transformados.
Estos tipos de transformaciones reciben el nombre de movimientos en el plano o Isometrías.
Tipos de movimientos:
Existen cuatro tipos de movimientos en el plano, la Traslación, el Giro o Rotación, la Simetría Axial y la Simetría con Deslizamiento. Cualquier movimiento en el plano es, necesariamente, uno de los cuatro anteriores.
Traslaciones y Giros se conocen como movimientos directos por conservar la orientación de la figuras mientras que las simetrías axiales y las simetrías con deslizamiento se conocen como movimientos inversos por no conservar la orientación de la figuras.
- La Traslación es un movimiento en el que los segmentos que unen un punto cualquiera y su transformado son siempre de la misma dirección sentido y longitud. El segmento, que está orientado por asignarle un sentido, se denomina vector de traslación
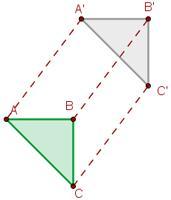
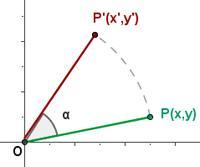
- El Giro de centro O y ángulo a es un movimiento en el que los segmentos que unen O con un punto cualquiera P y con su transformado P' son de la misma longitud y forman un ángulo igual a a.
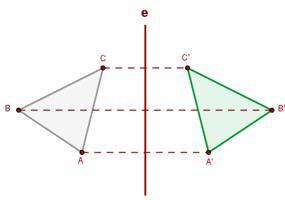
- La Simetría axial de eje la recta e es un movimiento en el que el eje e es mediatriz del segmento que une un punto cualquiera y su transformado, es decir, eje y el segmento se cortan perpendicularmente en el punto medio del segmento. Diremos que un punto A y su transformado A´ son simétricos respecto de e.
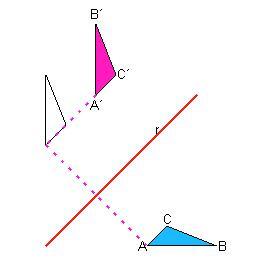
- La Simetría con deslizamiento es un movimiento que se compone de una simetría axial y de una traslación de vector paralelo al eje de simetría, es decir para transformar un punto determinamos su simétrico respecto de un eje y a continuación trasladamos el simétrico en dirección paralela al eje.
Si una figura (patrón) la repetimos mediante una traslación obtenemos un conjunto decorativo al que llamaremos friso o cenefa. Desde el punto de vista matemático sólo se pueden construir siete tipos de frisos esencialmente diferentes (son distintos al serlo los movimientos que los dejan invariantes). Partiendo de un motivo y realizando sobre él giros, simetrías o deslizamientos, obtenemos el patrón y como ya se ha dicho al trasladar éste obtenemos el friso.
Con estas mimbres se llega a la conclusión de que sólamente existen 7 tipos de frisos que explicamos a continuación, pero para ello es necesario introducir la notación básica que sirve para identificar y distinguir a los frisos. Se usa una p seguida de tres símbolos p _ _ _ :
- El primero será "m" si la cenefa contiene simetrías verticales y "1" si no las tiene.
- El segundo será "a" si hay deslizamientos, "m" si hay simetría horizontal y "1" en caso contrario.
- Y el tercero será "2" si hay giros y "1" si no los hay.
Para entenderlos mejor se ha puesto en cada uno un enlace a la web de Doña María Dolores Vela Arrans donde se explica cada uno usando el programa de geometría dinámica Geogebra.
- Primer tipo de Friso:
p111 -> Simetría de traslación

- Segundo tipo de Friso:
p112 -> Simetría de traslación y giros

- Tercer tipo de Friso:
p1m1 -> Simetría de traslación y simetría horizontal

- Cuarto tipo de Friso:
p1a1-> Simetría de traslación y deslizamiento Si quiere saber más
- Quinto tipo de Friso:
pm11-> Simetría de traslación y simetría vertical

- Sexto tipo de Friso:
pma2 -> Simetría de traslación, simetría vertical y deslizamiento

- Séptimo tipo de Friso:
pmm2 -> Simetría de traslación, simetría vertical y horizontalSi quieres saber más
Os dejamos para finalizar esta entrada un ejercicio solucionado para practicar con los distintos tipos de frisos. Ver
Referencias de webs usadas:
- http://www.iescomercio.edurioja.org/file.php/1/Proyectos/Russell_en_%20Atenas/teselaciones.htm
- http://platea.pntic.mec.es/curso20/123_geogebra/2010/M_Dolores_Vela/frisos.htm
