En una entrada anterior del blog hablé sobre la función cuadrática y, partiendo de su expresión más sencilla, y = x2, fui haciéndole transformaciones hasta llegar a la forma canónica de la función cuadrática general, de la que como conté se podía extraer directamente bastante información de su representación gráfica, es decir, de su parábola asociada:
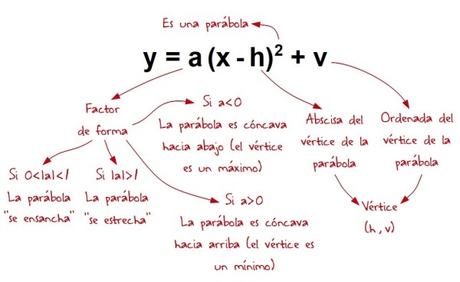
Si quieres ver la entrada completa éste es el enlace:
Función cuadrática (parábola). Parte I: Forma canónica
Aquella entrada la terminaba diciendo que me habían faltado más cosas por contar, y entre ellas estaba relacionar todo lo que se había visto con la expresión general de la ecuación cuadrática.
Pues eso es lo que voy a hacer en esta entrada.
La expresión general o forma desarrollada o polinómica de una función cuadrática es la siguiente:
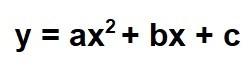
Ahora podría contaros directamente cómo se obtiene el vértice de la parábola a partir de los coeficientes de esta expresión, pero creo que no estaría aportando nada a lo que ya podéis ver en tantos sitios y prefiero que lo deduzcamos juntos.
Lo mejor es partir de la forma canónica (de la que ya sabemos bastantes cosas), desarrollarla y comparar lo que nos salga con esta expresión que acabamos de ver para sacar nuestras propias conclusiones.
No quiero que os perdáis en el camino, simplemente es un desarrollo. lo importante son las conclusiones que vamos a sacar después.
Partimos entonces de la forma canónica:
y = a·(x-h)2 + v
desarrollando el binomio al cuadrado…
y = a·(x2+h2-2·x·h) + v
aplicando la propiedad distributiva del producto respecto de la suma…
y = ax2 + ah2 – 2ahx + v
y colocando términos, tenemos:
y = ax2 – 2ahx + ah2 + v
Si ahora comparamos esta expresión con la polinómica, tenemos que:
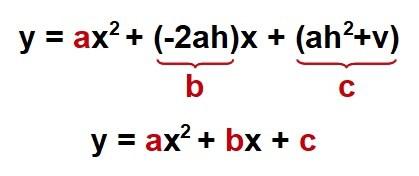
De donde deducimos que:
b = -2ah
c = ah2 + v
Pues a partir de ambas expresiones podemos obtener las coordenadas del vértice de la parábola en función de los coeficientes a, b y c.
Despejando h en la primera expresión obtenemos la abscisa del vértice de la parábola:
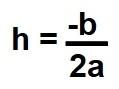
Despejando ahora v en la segunda expresión y sustituyendo después h por el valor anterior obtenido, conseguimos la ordenada del vértice de la parábola:
v = c – ah2
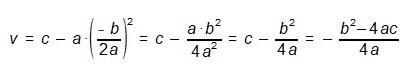
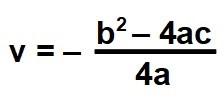
Es decir, el vértice de la parábola de la función cuadrática de ecuación desarrollada o polinómica y=ax2+bx+c es:
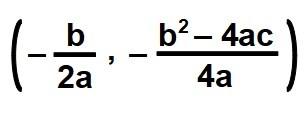
No te preocupes, porque esto es más sencillo de lo que parece, y en breve lo vamos a ver con un ejemplo y a modo de resumen como hice con la forma canónica.
Como has observado, esta forma desarrollada o polinómica no nos da directamente las coordenadas del vértice de la parábola, como sí lo hacía la forma canónica, aunque las podemos calcular a partir de los coeficientes a, b y c. Sin embargo sí nos da una información directa a través del coeficiente c que no nos daba la forma canónica: el punto de corte con el eje Y o eje de ordenadas, que sería el punto (0, c).
Esto que acabo de decir se deduce fácilmente ya que dicho punto es el que tiene como abscisa x=0, y si evaluamos la función en x=0 tenemos que:
y = 0·x2+0·x+c
y = c
Además seguimos teniendo la información que vimos que proporcionaba el coeficiente a en la forma canónica.
Resumiendo todo lo visto, a partir de la ecuación desarrollada o polinómica de una función cuadrática, podemos extraer la siguiente información:
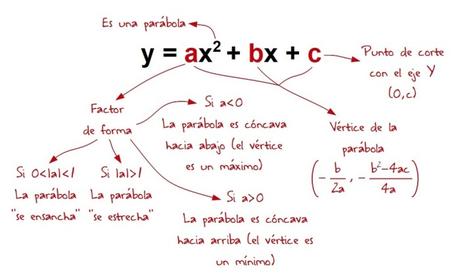
Por ejemplo, si tenemos la función:
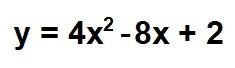
Podemos deducir que…
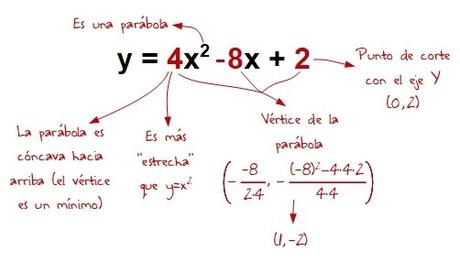
… tan solo echando cuentas para calcular el vértice.
Y ésta sería su representación gráfica:
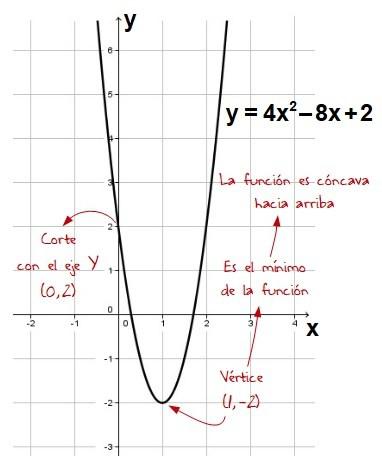
Bueno, espero con estas dos entradas haberte ayudado a entender mejor la función cuadrática.
Suscríbete al blog por correo electrónico
¡No te pierdas nada! Suscríbete de forma totalmente gratuita y recibirás un aviso a tu email cada vez que se publique una nueva entrada.
Únete a otros 2.394 suscriptores
Dirección de correo electrónico
La entrada Función cuadrática (parábola). Parte II: Forma desarrollada o polinómica se publicó primero en matematicascercanas.

