Función par y función impar. Estudiar la simetría de una función

Entre los distintos tipos de simetría que pueden presentar algunas funciones, las simetrías que tienen un mayor interés y que son de mayor utilidad a la hora de representar funciones son las de las que conocemos como funciones pares y funciones impares.

Cuando una función f  tiene una simetría axial respecto del eje de ordenadas, eje Y, decimos que es una función par, y en ella se cumple para todo su dominio que:

f(-x) = f(x)

Ejemplo de función par.

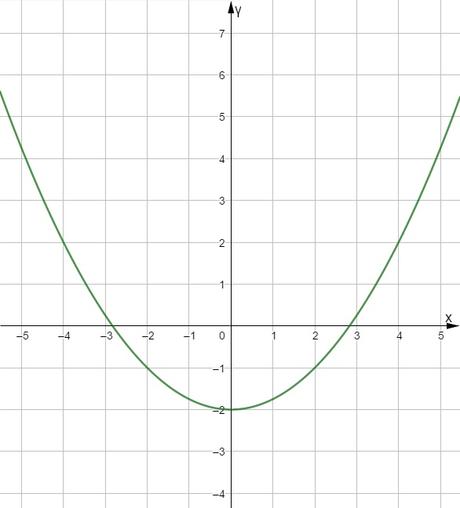
Sin embargo, cuando una función f  presenta una simetría central respecto del origen de coordenadas, O, decimos que es una función impar, y en ella se cumple para todo su dominio que:

f(-x) = – f(x)

Ejemplo de una función impar.

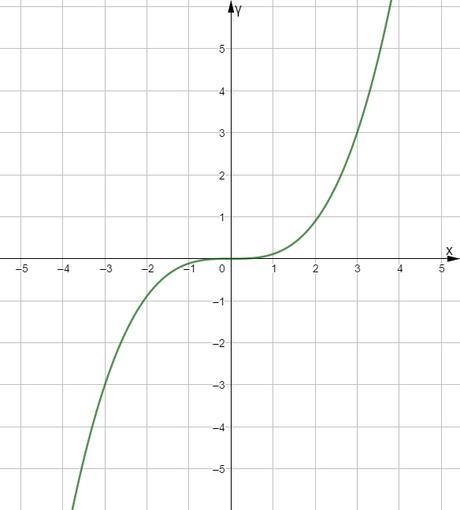
Si sabemos que una función es par o impar, conociendo o teniendo representada una mitad de ella (a un lado u otro del eje de ordenadas) podemos representar directamente la otra mitad.

Por esa razón es muy útil saber estudiar la simetría de una función, es decir, saber determinar de forma analítica a partir de su expresión si una función es par, impar o no presenta ninguno de estos dos tipos de simetría.

En el siguiente vídeo os hablo un poco más de las funciones pares e impares, y explico a través de varios ejemplos cómo podemos estudiar si una función es par, impar o ninguna de las dos.

---

Únete a otros 4.796 suscriptores

Dirección de correo electrónico

Suscribirme