Las funciones afines son funciones de la forma:
y = mx + n
Su representación gráfica es una recta.
En la expresión anterior, m es la pendiente de la recta y n es la ordenada en el origen.
Un ejemplo de función afín sería:
y = 2x + 1
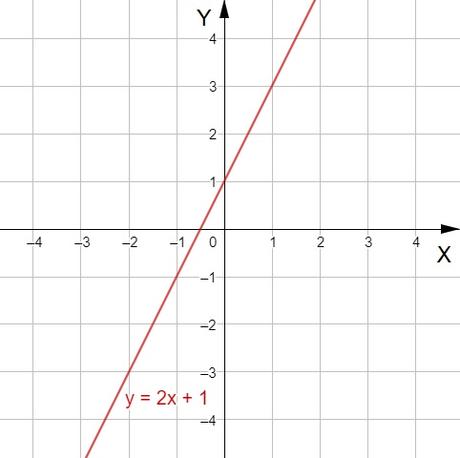
La pendiente es la tangente del ángulo que forma la recta con el eje X. Dicho de otra forma, es lo que aumenta (si la recta es creciente) o disminuye (si la recta es decreciente) la y (en vertical) cuando avanzamos una unidad en las x (en horizontal).
La ordenada en el origen nos indica dónde corta la recta al eje Y (eje vertical), y es la ordenada (coordenada y) del punto de corte de la recta con el eje Y.
Cuando la ordenada en el origen n es cero, la función es de la forma:
y = mx
y es una función lineal.
Su representación gráfica es una recta que pasa por el origen de coordenadas.
Un ejemplo de función lineal es:
y = 3x
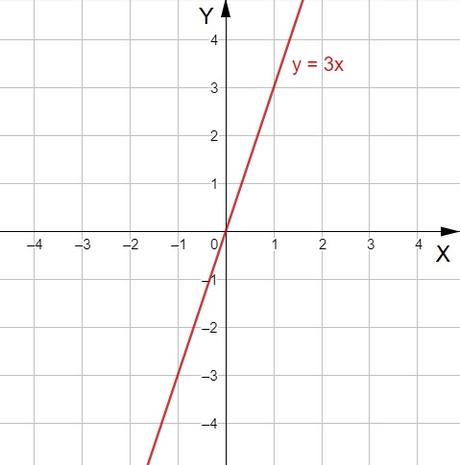
Si la pendiente m es cero, la expresión de la función es:
y = n
Para cualquier valor de x el valor de la función es siempre el mismo, y por eso, a este tipo de funciones se las llama funciones constantes.
La gráfica de una función constante es una recta paralela al eje X.
Un ejemplo de función constante es:
y = 3
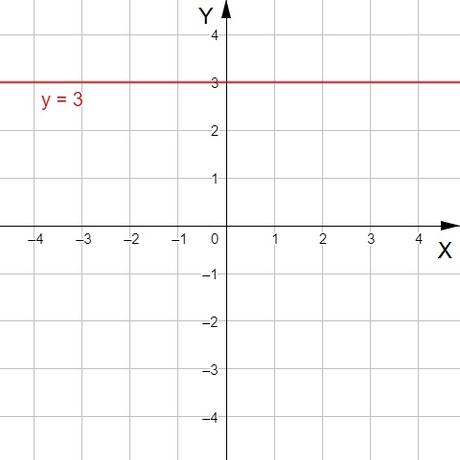
En el siguiente vídeo vamos a ver con mucho más detalle las funciones afines, las funciones lineales y las funciones constantes. Aprenderemos los conceptos básicos: Pendiente de la recta, ordenada en el origen, a distinguir unas funciones de otras, y a deducir la ecuación de cada función a partir de su gráfica:
¿Te ha gustado? No te pierdas ninguna entrada del blog y suscríbete a los avisos por correo electrónico. Sabrás al instante cuándo se ha publicado una entrada nueva.
Dirección de correo electrónico
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure