Gödel y los límites de la razón

Versión en PDF

El teorema de la incompletud de Gödel para los sistemas matemáticos se puede extender a los hechos consuetudinarios que acontecen en la rúa con un ejemplo tal que así: no es posible demostrar que la afirmación “este enunciado es falso” es verdadera.

Allá por la década de  1920, el Círculo de Viena, un colectivo inspirado por el pensamiento Ernst Mach, estaba convencido de que toda la realidad podía ser explicada desde la lógica formal y la observación empírica. Pero no les duraría mucho la ilusión de perfección. Kurt Gödel les demostró que había sucesos en el mundo que se escapaban a tales preceptos: la lógica formal demuestra que todo cuanto es verdadero dentro de un sistema dado es verdadero dentro de ese sistema, no que todo cuanto es verdadero pueda ser demostrado.

Es decir, hay verdades que se escapan al pensamiento racional. Por otra parte, éste se basa en demostraciones, pero una demostración se basa en condiciones: una conclusión es verdadera “si” los axiomas –los principios “obvios” en los cuales se basa—son verdaderos. Por tanto, afirmar algo como verdadero necesita no sólo de las pruebas, sino de la demostración de que los axiomas son efectivamente verdaderos.

En todo sistema, la demostración de los axiomas se descuida por necesidad, pues se considera que su verdad es evidente. Por ejemplo, un axioma que dirigió durante siglos el saber de los hombres fue el hecho cierto de que la Tierra era plana y, algo que duró más tiempo como axioma, el centro del universo.

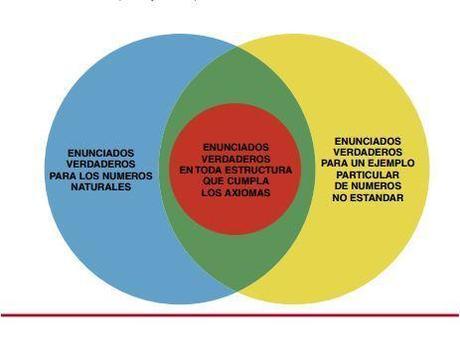
(Imagen: Investigación y Ciencia, agosto 1999)

En 1931, Gödel comunicó su teorema de incompletitud, según el cual existen enunciados sobre los números naturales que son verdaderos pero no pueden ser demostrados. Es decir, hay entidades que siguen las leyes de los números naturales, pero también obedecen otras que no se extraen de los axiomas del sistema: son los “números no estándar”, números que además de tener las mismas propiedades que los números naturales, tienen además otras ajenas al sistema establecido; puesto que tales propiedades no forman parte del sistema de axiomas, no pueden ser demostradas por ningún enunciado que parta de los principios establecidos como verdaderos: cualquier demostración de verdad en ese sentido tendría que referirse a algún principio más fuerte que los propios axiomas que conforman el sistema.

El pensamiento de Gödel sentó las bases para el desarrollo de la ciencia de la computación. Hoy, por ejemplo, una aplicación del teorema de incompletitud en informática es que ningún programa que no altere el sistema operativo de un ordenador podrá detectar los programas-virus que sí lo hacen.

Del teorema de incompletitud, Gödel extrajo un corolario, y es que, ya que ningún sistema consistente puede demostrarse desde dentro del propio sistema, sólo un sistema inconsistente es capaz de demostrar que es consistente.

A día de hoy, la teoría de la información dice que hay un número infinito de teoremas matemáticos que son verdaderos pero que no pueden demostrarse mediante un sistema finito de axiomas. O, lo que es lo mismo, el homo sapiens jamás podrá conocer la verdad de las cosas con absoluta certeza. No, al menos, mediante el recurso racional del lenguaje.

Según afirmara en su día Leibniz, una teoría tiene que ser más sencilla que los hechos que explica, o de lo contrario no explicaría nada. Esta idea es la base de la teoría algorítmica de la información. Mientras que la medida de la información consiste en determinar los bits necesarios para codificar un mensaje –por ejemplo, para una respuesta basada en un “sí” o un “no” se necesita un bit, el cual tiene dos estados posibles codificados como 1 y 0; si se añade un “depende”, harían falta dos bits combinados 00 para “no”, 11 para “sí”, 10 o 01 equivalentes para “depende”—, la teoría algorítmica se preocupa por encontrar la expresión más sencilla para codificar un mensaje.

Pero hay mensajes para los que no existen expresiones más sencillas que ellos mismos; por ejemplo, hay un algoritmo que contiene el valor completo del número pi, no hay que escribir sus infinitos decimales para expresarlo en su totalidad –otra cosa es el tiempo (infinito por otra parte) que lleve al procesador mental o computacional “desempaquetar” tal información; pero no existe algoritmo para expresar un número cogido al azar que contenga mil millones de decimales, por ejemplo, salvo que expresemos el número en sí con sus mil millones de decimales. Aquí, el hecho que se quiere explicar no encuentra una teoría más sencilla que realmente lo explique.

Una teoría científica busca ser el algoritmo más sencillo que expresa una información, en este caso una realidad determinada del mundo físico; todo algoritmo contiene la totalidad de la información de una entidad, como el ejemplo del número pi, y por ello su aplicación permite conocer, predecir y manipular dicha entidad. La ciencia sigue el precepto de Leibniz, de modo que, cuanto más sencillo sea el algoritmo, se entiende que mejor se ha comprendido esa realidad. Sin embargo, también se topa con hechos de la realidad irreductibles a algoritmos sencillos.

Hay otro principio de Leibniz seguido por el pensamiento científico: el principio de la razón suficiente, según el cual todo lo que ocurre tiene una razón, una causa. Este principio es, precisamente, el que mueve al pensamiento científico tradicional al exigir una demostración formal de cualquier suceso. En realidad, la causalidad mueve a todo pensamiento, sólo que éste en concreto lo reduce a causas formales.

Pero el concepto de “axioma” lleva implícita en su definición la irreductibilidad lógica, pues es verdadero por sí mismo sin razón suficiente. Para colmo, al ser evidentes, los axiomas no requieren una teoría más sencilla que los explique; si no se da una teoría más sencilla que explique un evento, entonces ese evento no puede ser lógicamente comprendido.

Si el principio de razón suficiente se desmorona en los fundamentos últimos de la realidad, es porque la razón no alcanza a explicar la realidad en su totalidad: la realidad es irracional en su esencia; la razón es un producto que emerge de una irracionalidad que todo lo abarca. Hay verdades que jamás serán conocidas y convencionalismos consensuados como verdades.

La única vía que parece quedar, pues, es la fuerza de la costumbre; consolidado el sistema mediante principios que parecen no fallar, esto es, que resultan evidentes, se los afirma como axiomas, confiando en ellos mientras no surjan problemas.

Para Gödel, no es posible automatizar el proceso de deducción por lo que, desde su punto de vista, hacía falta recurrir a la intuición en la investigación matemática; para él esto era sencillo, pues creía en la existencia de un mundo de conceptos, al estilo platónico, y a ese mundo no es posible acceder desde la razón sometida al sistema establecido, sino mediante la intuición creativa que lo supera.

Sólo cabe una terrible y desgarradora conclusión: el pensamiento científico, tal y como se lo concibe y limita hoy en los ambientes más influyentes, respetados y admirados de nuestra civilización en progresiva decadencia, es decir, reducido a la lógica formal y a filosofías materialistas, no deja de ser, para desgracia de todos, otra pseudociencia más que añadir al largo historial de las supersticiones humanas.

Pero seamos optimistas, pues la Ciencia está muy por encima de los reduccionismos de que gustan los terrícolas. Tarde o temprano, habrán de surgir quienes la liberen de las cadenas de lo superficial.

Relacionado