Gravity: Escombros

Aunque en el primer post dedicado a Gravity mencioné que quería explicar dos errores importantes, los comentarios me han animado a tratar un tercer error, que también es parte fundamental de la trama. Me refiero a los escombros en sí, tras la destrucción del satélite ruso.

Como siempre, vamos primero a recordar lo que vemos en la película. Houston informa a los astronautas de que los rusos han destruido un satélite propio con un misil (algo bastante irresponsable, pero teniendo en cuenta el mundo en el que vivimos, creible). Al principio parece que no hay peligro, pero a los pocos minutos, Houston avisa que los restos del satélite han chocado con otros, provocando una reacción en cadena, y que deben abortar la misión inmediatamente. Al poco rato, vemos como un grupo de fragmentos choca contra el transbordador y desata el caos. Se mueven muy rápido, lo suficiente para causar daños terribles e imprimir una rotación considerable a la nave, pero no tanto como para que escapen a la visión del ojo humano. Se ve cómo se acercan, y se ven perfectamente cruzando la pantalla. Más adelante, el protagonista dice que los fragmentos volverán cada 90 minutos.

Bueno, lo primero que hay que tener en cuenta es que en una explosión, los fragmentos salen despedidos en todas direcciones. En nuestro planeta, tarde o temprano todos los fragmentos acaban aminorando y cayendo al suelo, debido al aire y la gravedad. Pero en el espacio profundo, los fragmentos mantendrían la velocidad inicial al no haber rozamiento. Además, todas las trayectorias serían rectas y divergentes desde el punto de la explosión, por lo que a medida que avanzan, se separan unos de otros. Es como un globo con puntos dibujados en su superficie, que se hincha. A medida que se hace más grande, la separación entre los puntos es mayor. Así que cuanto más lejos de la explosión, menos probabilidad hay de que te alcance un fragmento, aunque si lo hace, lo hará con la misma velocidad que tenía en el momento de la explosión.

Pero ¡cuidado! He dicho que eso es lo que ocurriría en el espacio profundo, lejos de cualquier campo gravitatorio, y suponiendo que el objeto destruido estaba en reposo con respecto a nosotros. En órbita, las cosas son algo distintas. El objeto que explota se mueve a gran velocidad a lo largo de una trayectoria curva, debido a la gravedad de nuestro planeta. Y las cosas cambian. Para entender qué ocurriría, hay que tener primero muy claras unas nociones básicas de mecánica orbital. Vamos a comenzar con las Leyes de Kepler:

Primera Ley: La órbitas son elipses, y el cuerpo orbitado está en uno de los focos. No olvidemos que la circunferencia es un caso particular de la elipse, en la que ambos focos coinciden en un único punto (el centro de la circunferencia). También conviene matizar que cuando el volumen del cuerpo orbitado no es despreciable, lo que está en el foco es el centro de gravedad de dicho cuerpo (en nuestro caso, el centro de la Tierra)

Segunda Ley: La línea imaginaria que une el cuerpo en órbita con el objeto orbitado (con el foco, en realidad), barre areas iguales en tiempos iguales. Esto implica que a menos que la trayectoria sea una circunferencia (donde la velocidad sería constante), la velocidad del objeto varía a lo largo de la misma, alcanzando su máximo en el punto de mínima distancia o perigeo, y su mínimo en el punto de máxima distancia o apogeo.

Tercera Ley: El cuadrado del periodo orbital (tiempo que tarda el objeto en dar una vuelta completa) es proporcional al cubo del semieje mayor de la elipse. Es decir, cuanto mayor sea la distancia en el apogeo, menor será la velocidad media del objeto.

Hay un detalle muy importante sobre el tema de la velocidad, que conviene tener también claro: La velocidad en un punto dado, depende no sólo de la distancia en ese punto, sino también de la forma de la trayectoria. Algo lógico si tenemos en cuenta que nos basta con conocer la posición y velocidad del objeto en un punto concreto, para calcular toda la trayectoria. O dicho de otro modo, para una posición y velocidad concretas, sólo existe una órbita posible.

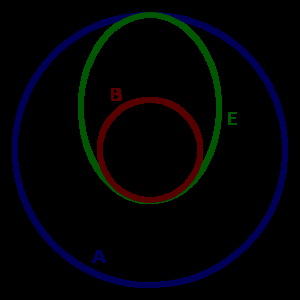
Ahora, ¿cómo afecta la velocidad? ¿Cómo varían órbitas que se tocan en un punto, pero con diferente velocidad? Bien, voy a comenzar con un ejemplo sencillo. Imaginad dos órbitas circulares a distinta altura, y en el mismo plano. Llamemos «A» (de alta) al objeto en la órbita más alta, y «B» (de baja) al objeto en la órbita más baja. Ambos objetos se mueven a velocidad constante (segunda ley), siendo mayor la de B (tercera ley, puesto que el semieje mayor de una circunferencia coincide con el radio de la misma). Imaginad ahora una órbita eliptica, también en el mismo plano, y que es tangencial a las dos anteriores. Esto es, su apogeo toca la órbita de A, y su perigeo toca la órbita de B. Llamemos «E» (de elíptica) a este objeto. El objeto E tiene mayor velocidad en el perigeo que en el apogeo (segunda ley), y en término medio, se moverá más despacio que B y más rápido que A (tercera ley, puesto que su semieje mayor es mayor que el radio de la circunferencia de B, y menor que el de la circunferencia de A).

Pero ¿y si lo comparamos la velocidad exacta de E en el apogeo y perigeo con la de A y B? Pues sucede algo muy curioso. En el perigeo (punto más cercano y rápido), la velocidad de E es mayor que la de B En el apogeo (punto más cercano y lento), la velocidad de E menor que la de A. Es decir, aunque la velocidad media de E está entre la de A y B, su velocidad máxima es mayor que la de B, y su velocidad mínima es menor que la de A. Recordad esto, que es muy importante para lo que sigue.

De momento nos estamos limitando a cuerpos en órbita, cuando sólo la fuerza de gravedad está actuando. ¿Qué ocurre cuando se ejerce una fuerza adicional, como la propulsión de un vehículo o el impulso de una explosión? Pues que la trayectoria se modifica. Una vez cesa dicha fuerza adicional, si no se ha alcanzado la velocidad de escape, la nueva trayectoria sigue siendo una elipse. Además, el punto en el que se dejó de ejercer la fuerza, pertenece a esta nueva elipse. Esto parece una perogrullada, pero implica algo que no hay que olvidar: Si no se vuelve a modificar la trayectoria, el objeto volverá periódicamente a ese mismo punto.

La forma en la que se modifica la elipse, hace que la mecánica orbital sea bastante antiintuitiva. Pero en el fondo no es tán difícil razonar sobre ello. Una fuerza aplicada se traduce en un cambio de velocidad, que no olvidemos, es un vector, esto es, tiene una dirección. Al final del proceso, lo único que nos importa es esa nueva velocidad (recordad que sólo necesitamos la posición y velocidad en un punto para calcular toda la trayectoria).

¿Qué ocurre aceleramos o deceleramos en la misma dirección? La dirección y sentido de la nueva velocidad es la misma, pero no su módulo (su intensidad). Estaremos cambiando la excentricidad de la órbita, y de una forma muy curiosa. Si aceleramos, estamos alejando la posición que tendrá nuestro objeto tras 180º de recorrido. Si frenamos, estaremos acercando esa misma posición. En el caso concreto de que hagamos la maniobra en el apogeo o perigeo, estaremos modificando la distancia del punto opuesto, sin modificar la orientación de los ejes de la elipse. Por ejemplo, si aceleramos en el apogeo de una órbita elíptica, estamos aumentando la distancia del perigeo, y por tanto, disminuyendo la excentricidad, pudiendo llegar a hacerla circular. O también, si aceleramos en una órbita circular, estaremos dándole excentricidad, y situando el apogeo en el punto opuesto de donde estamos. Así es como funcionan las órbitas de transferencia de Hohmann, para subir o bajar una órbita circular.

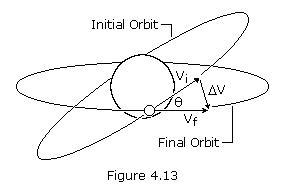
¿Qué ocurre si «viramos» a la izquierda o derecha? El módulo de la velocidad sigue siendo el mismo, pero la dirección ha cambiado en el plano horizontal (fijaos que para ello no basta con impulsar de forma lateral el objeto, sino que hay que decelerar la misma cantidad en la dirección original). La forma y tamaño de la órbita sería la misma, pero habremos cambiado su inclinación. Por ejemplo, si partimos de una órbita circular ecuatorial, podríamos obtener una órbita también circular y a la misma altura, pero con una inclinación de 15º.

¿Qué ocurre si «subimos» o «bajamos» en nuestra trayectoria? Es decir, ¿qué ocurre si damos un impulso radial hacia arriba o hacia abajo? El efecto es muy curioso, ya aunque obviamente estamos alejando o acercando ese punto en concreto hacia la Tierra, el punto opuesto (situado a 180º) siempre subirá, ya que en ambos casos estamos aumentando la velocidad total. Además, estaremos cambiando también la orientación de los ejes de la elipse.

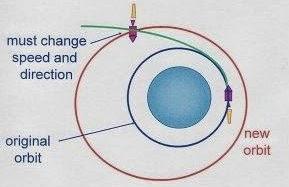
Todos estos casos están resumidos con dibujos, en SpaceTEC. Lo importante es darse cuenta de que tras la explosión, cada fragmento recibe un impulso en una dirección diferente, por lo que cada uno adopta una órbita diferente. Habrá órbitas de distinta excentricidad, distinto periodo y distinta inclinación. Además, todas las órbitas se cruzan en el punto de la explosión. No todos los fragmentos pasan por ese punto de cruce al mismo tiempo, ya que no todos tienen el mismo periodo, pero aquellos que sí lo tengan, podrían chocar, alterando nuevamente sus órbitas. Y por supuesto, en el caso de una reacción en cadena (un fragmento choca contra un satélite, lanzando más fragmentos al espacio), tendríamos aún muchas más fragmentos en diferentes órbitas.

No olvidemos tampoco las enormes velocidades que tienen. En el primer post que dediqué a la película, comenté que la velocidad del Hubble es de 27.000 km/h. Eso es 30 veces la velocidad de crucero de un avión comercial. O más de 20 veces la velocidad del sonido a nivel del mar. Si eso no os impresiona, pensad que el periodo orbital es de unos 90 minutos. Es decir, el Hubble da una vuelta alrededor de la Tierra cada hora y media. A esa velocidad, viajaríamos de Madrid a Barcelona en 67 segundos, esto es, poco más de un minuto. Es por eso que la basura espacial puede llegar a ser tan peligrosa. No por el tamaño del fragmento, sino por su velocidad.

En la película nos muestran algo totalmente diferente. Lo primero que llama la atención es que el movimiento de los fragmentos es visible. No tienen la vertiginosa velocidad que he mencionado. Bueno, podría ocurrir que estuvieran en una órbita muy similar a la de los protas, de forma que la diferencia de velocidad no fuera tan grande.

El problema está en que vemos un grupo de fragmentos juntos, en la misma trayectoria. Eso no es posible. Los fragmentos deberían haber salido en distintas direcciones, separándose rápidamente. Recordad que tada uno de ellos debe seguir una trayectoria diferente. Además, el hecho de que periódicamente vuelvan a pasar, sólo es aplicable si mantenemos nuestra órbita, y nuestro periodo orbital es el mismo que el de los fragmentos. Una vez modifiquemos nuestra órbita (y los protas lo hacen al ir a la ISS), esos fragmentos en concreto ya no son una amenaza, aunque pueden serlo otros en otras órbitas.