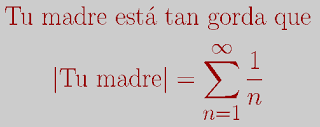Hasta el infinito con la serie armónica

Cuando un alumno se enfrenta por primera vez a las series, es decir, a las sumas infinitas, se encuentra con numerosos momentos en los que la lógica parece no funcionar bien. Y no hay que irse a series extrañas o formas diferentes de sumar números naturales, por ejemplo.
¿Es posible que sumando cosas cada vez más pequeñas al final lleguemos al infinito? Dicho en lenguaje matemático, ¿existen series divergentes cuyo término general tiende a cero? La respuesta es que claro que sí. Y seguro que te ha venido a la mente EL EJEMPLO clásico: La serie armónica. En este artículo vamos a ver alguna forma de probar que la serie armónica es divergente.

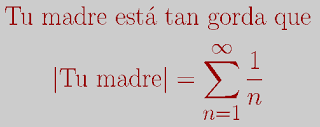
Idea extraída de aquí

Una de las demostraciones más sencillas se apoya en la relación que hay entre series e integrales.
Llamemos a la suma parcial enésima de la serie armónica. 
Comencemos hablando un poco del logaritmo:
<%20%5Csum_%7Bk=1%7D%5En%5Cint_k%5E%7Bk+1%7D%5Cfrac%7B1%7D%7Bk%7D%5C,%20dx=%5Csum_%7Bk=1%7D%5En%5Cfrac%7B1%7D%7Bk%7D=H_n"><%20%5Csum_%7Bk=1%7D%5En%5Cint_k%5E%7Bk+1%7D%5Cfrac%7B1%7D%7Bk%7D%5C,%20dx=%5Csum_%7Bk=1%7D%5En%5Cfrac%7B1%7D%7Bk%7D=H_n"><%20%5Csum_%7Bk=1%7D%5En%5Cint_k%5E%7Bk+1%7D%5Cfrac%7B1%7D%7Bk%7D%5C,%20dx=%5Csum_%7Bk=1%7D%5En%5Cfrac%7B1%7D%7Bk%7D=H_n" style="display: inline;" alt="[;\log(n+1)=\int_1^{n+1}\frac{1}{x}\,dx =\sum_{k=1}^{n}\int_{k}^{k+1}\frac{1}{x}\,dx < \sum_{k=1}^n\int_k^{k+1}\frac{1}{k}\, dx=\sum_{k=1}^n\frac{1}{k}=H_n;]" title="\log(n+1)=\int_1^{n+1}\frac{1}{x}\,dx =\sum_{k=1}^{n}\int_{k}^{k+1}\frac{1}{x}\,dx < \sum_{k=1}^n\int_k^{k+1}\frac{1}{k}\, dx=\sum_{k=1}^n\frac{1}{k}=H_n" />  Por tanto, tenemos que %5Clog(n+1)" />%5Clog(n+1)" />%5Clog(n+1)" />%5Clog(n+1)" style="display: inline;" alt="[;H_n>\log(n+1);]" title="H_n>\log(n+1)" />, de donde se deduce que
 
Vale, esta demostración es un poco tramposa precisamente porque hace uso de la relación entre integral y serie. De hecho no muestra realmente cómo se produce la divergencia. Vamos a ver ahora otra demostración muy sencilla que extraje de la web de Leo Goldmakher (concretamente de aquí).
Supongamos, por reducción al absurdo, que la serie armónica es convergente y que su suma es , es decir,  En general se tiene que 1/(n+1)" />1/(n+1)" />1/(n+1)" />1/(n+1)" style="display: inline;" alt="[;1/n>1/(n+1);]" title="1/n>1/(n+1)" />, por lo que podemos afirmar que1+%5Cfrac%7B1%7D%7B2%7D+%5Cleft(%5Cfrac%7B1%7D%7B4%7D+%5Cfrac%7B1%7D%7B4%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B6%7D+%5Cfrac%7B1%7D%7B6%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B8%7D+%5Cfrac%7B1%7D%7B8%7D%5Cright)+%5Ccdots" />1+%5Cfrac%7B1%7D%7B2%7D+%5Cleft(%5Cfrac%7B1%7D%7B4%7D+%5Cfrac%7B1%7D%7B4%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B6%7D+%5Cfrac%7B1%7D%7B6%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B8%7D+%5Cfrac%7B1%7D%7B8%7D%5Cright)+%5Ccdots" />1+%5Cfrac%7B1%7D%7B2%7D+%5Cleft(%5Cfrac%7B1%7D%7B4%7D+%5Cfrac%7B1%7D%7B4%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B6%7D+%5Cfrac%7B1%7D%7B6%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B8%7D+%5Cfrac%7B1%7D%7B8%7D%5Cright)+%5Ccdots" />1+%5Cfrac%7B1%7D%7B2%7D+%5Cleft(%5Cfrac%7B1%7D%7B4%7D+%5Cfrac%7B1%7D%7B4%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B6%7D+%5Cfrac%7B1%7D%7B6%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B8%7D+%5Cfrac%7B1%7D%7B8%7D%5Cright)+%5Ccdots" style="display: inline;" alt="[;H>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{6}+\frac{1}{6}\right)+\left(\frac{1}{8}+\frac{1}{8}\right)+\cdots;]" title="H>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{6}+\frac{1}{6}\right)+\left(\frac{1}{8}+\frac{1}{8}\right)+\cdots" />Si ahora sumamos cada paréntesis llegamos a que1+%5Cfrac%7B1%7D%7B2%7D+%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B3%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B4%7D%5Cright)%5Cdots=%5Cfrac%7B1%7D%7B2%7D+H>H" />1+%5Cfrac%7B1%7D%7B2%7D+%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B3%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B4%7D%5Cright)%5Cdots=%5Cfrac%7B1%7D%7B2%7D+H>H" />1+%5Cfrac%7B1%7D%7B2%7D+%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B3%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B4%7D%5Cright)%5Cdots=%5Cfrac%7B1%7D%7B2%7D+H>H" />1+%5Cfrac%7B1%7D%7B2%7D+%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B3%7D%5Cright)+%5Cleft(%5Cfrac%7B1%7D%7B4%7D%5Cright)%5Cdots=%5Cfrac%7B1%7D%7B2%7D+H>H" style="display: inline;" alt="[;H>1+\frac{1}{2}+\left(\frac{1}{2}\right)+\left(\frac{1}{3}\right)+\left(\frac{1}{4}\right)\dots=\frac{1}{2}+H>H;]" title="H>1+\frac{1}{2}+\left(\frac{1}{2}\right)+\left(\frac{1}{3}\right)+\left(\frac{1}{4}\right)\dots=\frac{1}{2}+H>H" />lo que nos lleva a una clara contradicción. Por lo que la serie armónica no puede ser convergente.
Tal y como apunta el autor de esta demostración, tiene una ventaja con la demostración clásica. En ella, se van agrupando cada vez más términos (de una potencia de 2 a la siguiente) y esto puede hacer que el alumno se pierda. En esta versión, se agrupan términos de 2 en 2, lo que hace las cosas algo más sencillas.
Ya vosotros elegís lo que os gusta más. Yo ya he cumplido. A disfrutar.
Tito Eliatron Dixit
PD: Esta entrada participa en la Edición 6.9: Conjunto de Cantor del Carnaval de Matemáticas cuyo anfitrión es el blog ::ZTFNews.org.  
 
Esta entrada se ha publicado originalmente en Tito Eliatron Dixit.
Si la estás viendo en otra web, probablemente estéás siendo víctima de un engaño.