Historias de Pi: de la geometría al número

Como todos sabemos, π es la relación entre la longitud de una circunferencia y su diámetro. Una definición puramente geométrica. Vamos a hablar de esta curiosa relación que impregna las matemáticas.

La definición de círculo aparece en el Libro I de Los Elementos; dice Euclides:

Definición 15. Un círculo es una figura plana comprendida por una sola línea (llamada circunferencia) de tal modo que todas las rectas dibujadas que caen sobre ella desde un punto de los que están dentro de la figura son iguales entre sí.

Definición 16. Y el punto se llama centro del círculo.

Definición 17. Un diámetro de un círculo es una recta cualquiera que pasa por el centro y que acaba en ambas direcciones en la circunferencia del círculo; esta línea recta también divide el círculo en dos partes iguales.

Y añade este postulado:

Postulado 3. Hay una sola circunferencia con un centro y un radio dados.

Desde el punto de vista puramente geométrico, la pregunta que uno se debería hacer es esta: ¿Por qué el cociente entre la longitud de una circunferencia dada y su diámetro es una constante?

A simple vista, parece bastante intuitivo. Si aplicamos un zoom a una circunferencia, vemos como la forma no cambia y a medida que va aumentando, el diámtro también lo hace, y lo mismo si disminuyéramos el tamaño. Pero claro, esto no es una demostración.

Vamos a mostrar algunas demostraciones que circulan por la red.

Dados dos círculos concéntricos como en la figura 1, tales que el radio del más pequeño es r, mientras que el del más grande es R. Sus circunferencias tienen longitudes c y C, respectivamente. Dibujamos dos segmentos desde el centro hasta formar los dos triángulos de la figura, que serán semejantes, ya que la proporción de los lados es la misma y tienen el ángulo común α.

Figura 1

Por lo tanto,  las cuerdas guardarán la misma proporción. Si β es el ángulo de  que corresponde al círculo completo ( 360^o ), entonces β/α . k = β/α . K , donde k y K son las longitudes de las espectivas cuerdas. Entonces, c/C se aproximaría a r/R, y si ahora ahora α  se fuera haciendo cada vez más pequeño, serían iguales. En conclusión, c/r = C/R.

Esta demostración padece de cierta rigurosidad, pero da una idea. Se puede proponer otra parecida basada en considerar polígonos inscritos en cada una de las circunferencias y también usar un argumento de paso al límite. Este razonamiento es similar al que usó Arquímedes para demostrar la afirmación similar relativa a la relación de las áreas de dos círculos en relación con los cuadrados de los radios respectivos.

Por supuesto, lo más riguroso sería considerar la fórmula para la longitud de un arco. En nuestro caso, el teorema de Pitágoras (Figura 2) nos dice que la función que define la circunferencia es

f(x) = √r² –x²

y de ahí integramos la función longitud de arco

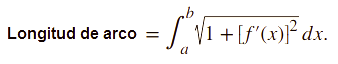
entre –r y r.

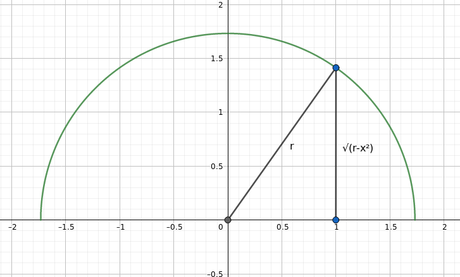
Figura 2

El resultado (tras un cambio de variable) nos dirá que esa longitud es s = r c₀ , donde c₀  es una cosntante que no depende de r. En consecuencia, la longitud de esta circunferencia arbitraria será

C = 2 s = 2 c₀ r

y por lo tanto  la relación entre la longitud de una circunferencia y su diámetro es constante, precisamente c₀ (que no es más que el número π.

___________

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).