Historias de pi: los calculadores

En entradas anteriores (De la geometría al número y Calculando el área del círculo) hemos visto como π era la relación entre la longitud de una circunferencia y su diámetro, y como se fue identificando su naturaleza a lo largo de los siglos hasta definirlo como un número irracional y trascendente. Nos ocuparemos hoy de los esfuerzos para calcular su valor aproximado.

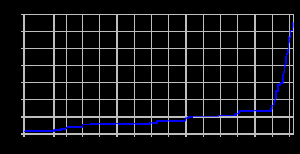
Gráfico mostrando el progreso en el cálculo decimal de pi

Las primeras aproximaciones escritas de π se encuentran en Babilonia y Egipto. En Babilonia, una tablilla de arcilla fechada entre 1900 y 1600 a.C. tiene un enunciado geométrico en el que se calcula π como 25/8 = 3,125. En Egipto, el Papiro Rhind, al que se le supone una antigüedad de unos 1800 a.C., presenta una fórmula de aproximación para el área de un círculo en la que π se toma como el doble de 16/9, aproximadamente 3,16 (el área de un círculo es similar a la de un cuadrado cuyo lado es igual al diámetro del círculo disminuido en 1/9). Por su parte, los matemáticos indios, alrededor del siglo IV a.C. dan un valor de 339/108 ≈ 3,139.  Las matemáticas chinas, tan desconocidas, parece ser que usaban el valor aproximado de 3, pero también se encuentran una aproximación como raíz cuadrada de 10 y 3,14 (la historia de π y las matemáticas chinas merecen una entrada propia en este blog).

Uno de los documentos más antiguos en la propia Biblia. En el Libro I de los Reyes, se lee

Hizo el Mar de metal fundido que tenía diez codos de borde a borde; era enteramente redondo, y de cinco codos de altura; un cordón de treinta codos medía su contorno. Debajo del borde había calabazas todo en derredor; daban vuelta al Mar a largo de treinta codos; había dos filas de calabazas fundidas en una sola pieza.

y en el Libro II de las Crónicas

Hizo el Mar de metal fundido, de diez codos de borde a borde. Era enteramente redondo y de cinco codos de alto. Un cordón de treinta codos medía su contorno.

Ambos textos arrojan un valor aproximado para π de 3, lejos de las aproximaciones previas.

Hemos comentado en entradas anteriores las aproximaciones de Arquímedes mediante polígonos inscritos, aunque, obviamente, la geometría tenía sus límites. El último gran intento de calcular π por este método fue realizado por el jesuita matemático y astrónomo austríaco Christoph Grienberger en 1630, quien calculó 39 decimales de π utilizando una mejora trigonométrica debida al matemático holandés Willebrord Snell.

Otros métodos recurren a la trigonometría, por ejemplo a fórmulas del tipo de la obtenida por John Machin en 1706:

π/4 = 4 arctan (1/5) – arctan (1/239)

con las que llegó a aproximar 100 cifras decimales. Con fórmulas similares, se ha llegado a aproximar π hasta con 1.241.100.000.000 dígitos.

John Machin

Expresar π como suma de una serie es otra de las técnicas para encontrar más y más decimales, y en esto Srinisava Ramanujan fue un auténtico genio:

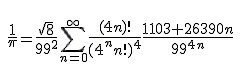
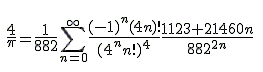
Srinivasa Ramanujan

Las expansiones decimales de π suelen calcularse con fórmulas iterativas como el algoritmo de Gauss-Legendre y el algoritmo de Borwein. El algoritmo de Chudnovsky es otro método rápido para calcular los dígitos de π, basado en las fórmulas de Ramanujan.

Se han escrito también programas para calcular π a muchos dígitos en ordenadores personales. En nuestros días, la caza de decimales de π se ha convertido en un auténtico desafío.

Obviamente, antes de la llegada de los ordenadores era mucho más difícil calcular π, y como muestra decir que en el siglo XIX, William Shanks tardó 15 años en calcularlo con 707 decimales, aunque posteriormente se descubrió que había cometido un error y solo se le concedieron 527 decimales correctos. Con los ordenadores, la cuestión cambia radicalmente; de hecho, en 2019, en el día de π, Googe consiguió un record, ¡31,4 billones de decimales!

Uno de los mejores calculadores de π fue el japonés Yasumasa Kanada, fallecido el 11 de febrero de 2020, y profesor del Departamento de Ciencias de la Información de la Universidad de Tokio hasta 2015. Estableció el récord 11 de las últimas 21 veces.

Yasumasa Kanada

El récord lo tiene ahora Timothy Mullican, norteamericano de Huntsville, Alabama, quien obtuvo el 29 de enero de 2020 la friolera de 50 billones de dígitos utilizando el algoritmo de Chudnovsky. El cálculo le llevó más de 8 meses en total. Intentó este récord para poner a prueba los límites de su hardware y, durante el proceso de intento del récord, Timothy fundó una organización sin ánimo de lucro llamada North Alabama Charitable Computing, que reutiliza equipos de computación y almacenamiento de grado empresarial para la investigación STEM. Timothy tiene previsto donar el servidor y los discos duros utilizados en el intento para proporcionar potencia informática a los científicos y a diversos proyectos de investigación.

Timothy Mullican

Y si, el cálculo de los decimales de π se usa en computación para probar el hardware de los ordenadores.

___________

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).