Hace tiempo un amigo me comentó que había descubierto una estrategia para ganar seguro en las ruletas de los casinos. Esta era la estrategia de la martingala. A simple vista no tiene ningún defecto, se hace una apuesta a un color y cuando se gana se recogen los beneficios y se hace otra apuesta. Pero, cuando se pierde simplemente se dobla la apuesta para cubrir las pérdidas hasta volver a ganar. Solamente hay que tener fondos para soportar una mala racha. Lo que es justamente el problema de la estrategia, la existencia de malas rachas que obligan a aumentar la apuesta hasta cantidades impensables.
A continuación, se explicará el juego de la ruleta y la estrategia martingala. Realizando un análisis estadístico de esta. Además, para comprobar que no es una estrategia fiable al final de la entrada se explicará cómo hacer una simulación de Montecarlo.
El juego de la ruleta
La ruleta es un juego de azar típico de los casinos. Existen diferentes configuraciones entre las que destacan la ruleta francesa y la americana. Para ilustrar cómo funciona la estrategia de la martingala se va a utilizar únicamente la francesa. En esta existe 37 casillas numeradas de 0 a 36. Además, cada una de las casillas son de color rojo o negro, salvo el 0.
El jugador puede apostar por un número. En caso de que este sea el premiado recibirá como premio 36 veces lo apostado, en caso contrario perderá la apuesta. Como se puede ver la probabilidad de ganar es 1/37. Así al jugar se puede recuperar estadísticamente solamente 36/37, un 97,3%, de lo apostado, siendo el resto, 2,7%, el beneficio esperado para el casino.
Las apuestas sencillas son las que se juega en la estrategia martingala. En estas las apuestas son siempre sobre a opciones que cubre 18 casillas (rojo o negro, par o impar, falta o pasa). En ambos casos si se gana el premio es dos veces lo apostado. Salvo en los casos que el resultado sea cero donde se pierde lo apostado en todas las apuestas sencillas. La probabilidad de ganar jugando una apueste sencilla es 18/37, es decir, 48,6%, no del 50%. Por lo tanto, estadísticamente se recuperaría el 97,3% de lo jugado, quedando, al igual que la apuesta a un único número, un 2,7% para el casino.
La estrategia martingala
La estrategia martingala es sencilla: se apuesta una cantidad de dinero en una apuesta sencilla. Si se gana se recupera el doble, la mitad cubre la apuesta y la otra mitad es beneficio. En el caso de perder se apuesta el doble de la anterior, así al ganar con los beneficios se cubren las pérdidas anteriores y se obtiene un pequeño beneficio.
Asumiendo que las posibilidades de ganar son cercanas al 50% en cada ocasión solamente hay que soportar rachas negativas. Pero, si la esperanza matemática es del 97,3% ¿cómo es posible ganar? La respuesta es que una racha negativa es más probable de lo que aparenta intuitivamente.
Crecimiento del coste de las apuestas
La estrategia de martingala exige que en cada una de las apuestas se juegue el doble de la anterior. De este modo la cantidad a apostar en la jugada n después de perder n-1 veces es:
B_n = \sum_{t=1}^{n} b 2^{t-1} = b (2^n - 1)
Donde b es la apuesta inicial. Así las pérdidas acumuladas después de perder n veces es:
Así tras una racha de 5 jugadas perdidas se acumuladas de 57 veces la apuesta original, con 8 son 502 veces la original y con 10 son 2036 veces. Dado que en los casinos existen apuestas máximas, esto puede dar al traste con la estrategia. Si no lo da las pérdidas acumuladas.
Nótese que el beneficio esperado crece linealmente con el número de apuestas realizadas, mientras que las pérdidas lo hacen de forma exponencial. Por lo que cada vez los riesgos son mayores. Esto se puede apreciar viendo cómo crecen las rachas esperadas con el número de apuestas.
Probabilidad de una racha
La probabilidad de ganar una apuesta sencilla es de 18/37, no del 50%. Así la probabilidad de perder n apuestas seguidas es
Así hay un 3,6% de perder 5 veces seguidas, 0,5% de hacerlo 8 veces y 0,13% de hacerlo 10 veces. Probabilidades que son bajas, pero no nulas.
La racha más larga para una cantidad de apuestas de puede calcular utilizando la siguiente expresión:
Donde g es el número de apuestas realizadas y p_L es la probabilidad de perder. Así se puede esperar una racha de 5 en 25 jugadas, de 8 en 200 y de 10 en 600.
Simulación Montecarlo de un juego con martingala
La mejor forma de ver esto es con una simulación de Montecarlo. Para ello se puede utilizar el siguiente código de Matlab.
g = 10000;
b = 10;
max_bet = Inf;
streak = 0;
result = zeros(1, g);
for i = 1:g
% Apuesta en base a la racha
bet = b * 2^(streak - 1);
% Limitar la apuesta a la máxima permitida
if bet > max_bet
bet = max_bet;
end
% Simular una partida
if rand() < 18/37
streak = 0;
result(i) = bet;
else
streak = streak + 1;
result(i) = -bet;
end
end
plot(cumsum(result))
xlabel('Juegos');
ylabel('Beneficio acumulado');
if isinf(max_bet)
title('No hay apuesta máxima');
else
title(sprintf('Apuesta máxima %d', max_bet));
end
En este se utiliza g para indicar el número de apuestas, b para la apuesta base, y max_bet para la apuesta máxima permitida. Luego en la variable streak se almacena la racha actual y los resultados de cada apuesta en results.
Posteriormente en un bucle se realiza la simulación. En cada ocasión se hace una apuesta en función de la racha, pero si esta es mayor que el límite se apuesta únicamente lo permitido. Una vez fijada la apuesta se simula la jugada. En caso de ganar resultado es lo ganado y en caso contrario lo perdido. Así las pérdidas acumuladas se pueden reasentar en una gráfica. En caso de no existir un límite de apuesta máxima se tiene.
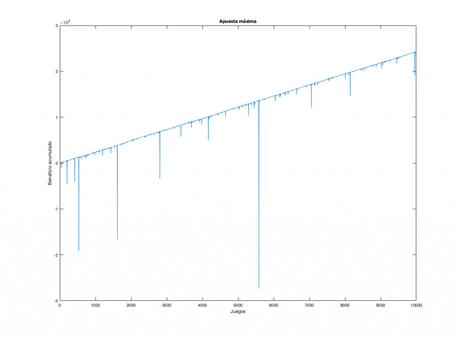
En este caso se puede ver que el beneficio esperado crece linealmente con las partidas. Pero si se puede asumir las pérdidas acumuladas en las diferentes rachas que suceden durante el juego. Por otro lado, si se fija un límite se puede obtener otro resultado diferente.
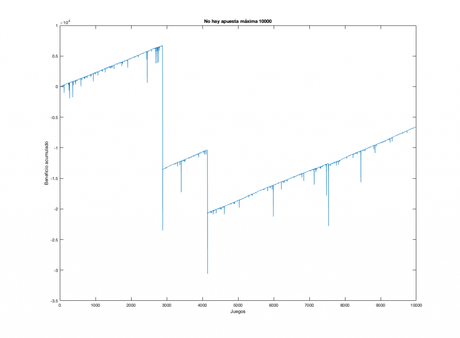
Ahora, al no poder recuperar lo perdido en las rachas, el beneficio esperado es negativo a medida que aumenta el número de apuestas.
Conclusiones
En esta entrada se ha visto la estrategia martingala. Una estrategia que intuitivamente parece fiable, pero que es debido a una mala estimación de las probabilidades de sufrir una racha. Como se ha explicado y visto en la simulación, solamente es válida si se pueden asumir pérdidas enormes durante el juego.
En los juegos de azar el organizador del mismo es el único que gana de forma sistemática. Algo que ya se ha visto en la entrada que se publicó sobre la Lotería de Navidad.
Imágenes: Pixabay (Greg Montani )
No te olvides valorar esta entrada
Suscríbete a nuestro boletín
Suscríbete al boletín semanal para estar al día de todas las publicaciones de Analytics Lane.
