Esta es nuestra cuarta entrada dedicada a la criptografía, continuando las tres anteriores “¿Estamos seguros?” y “El hombre que se enfrentó a la NSA” y “¿Cuánticamente seguros?”.
Nos hacemos la siguiente pregunta: ¿Qué cantidad n de números enteros aleatorios debemos tomar de un intervalo [1,N] para que la probabilidad de que dos de ellos sean iguales, sea 1/2? La respuesta es que n debe ser aproximadamente 1.18 √ N. Recordemos que un número aleatorio es aquel obtenido al azar, y existen muchos métodos para generarlos (por ejemplo, echando monedas al aire o tirando dados).
Esta pregunta podría ser una de esas que se hacen los matemáticos y que podíamos pensar que no sirven para nada útil. Sin embargo, su respuesta tiene numerosas aplicaciones prácticas en la ciencia de la computación y también en la criptografía, tal y como mostraremos a continuación.
En esta entrada veremos un ejemplo de cómo los ordenadores pueden detectar claves criptográficas y almacenar mensajes de manera correcta. En particular, el método que se describe es el de identificación de una clave.
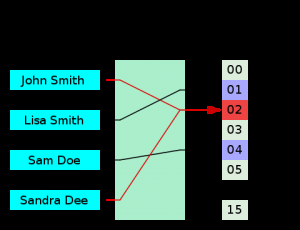
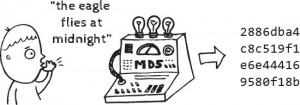
Un método común de identificación de claves es el método de las funciones hash. Una función hash produce cadenas arbitrarias de caracteres después de introducir un mensaje en una plataforma, por ejemplo, una clave alfanumérica, de manera que no se puede crear esa cadena a menos que se introduzcan los mismos datos. Al conjunto de entradas se le llama dominio U de la función hash. A un elemento de U se le llama preimagen o, dependiendo del contexto, clave o mensaje. El término hash proviene, aparentemente, de la analogía con el significado estándar en inglés de dicha palabra en el mundo real: picar y mezclar. Donald Knuth indica que aunque Hans Peter Luhn de IBM parece ser el primero que utilizó este concepto en 1953, el término sólo habría aparecido en la literatura a finales de los 60 del siglo XX.

Hans Peter Luhn
En este artículo “¿Qué son y para qué sirven los hash?: funciones de resumen y firmas digitales”, de Pedro Gutiérrez, puede encontrarse una valiosa información sobre el tema.
Las funciones hash se usan por ejemplo para proteger contraseñas, para garantizar la integridad de una descarga de datos, o para producir firmas digitales. No son propiamente métodos de encriptación, sino algoritmos.
Las funciones hash operan matemáticamente como una función f(x) que genera N resultados diferentes e igualmente probables. Si N es muy grande, sabemos que tras evaluar la función en 1.18 √ N elementos, tenemos una probabilidad de al menos ½ de que f(x1)=f(x2).
Se llama colisión cuando dos entradas distintas a la función producen la misma salida. El rango de la función es finito, debido a que el tamaño de sus cadenas de salida es fijo. Por tanto, la posibilidad de colisión no es nula. Una buena función de hash es aquella en que las colisiones son las mínimas. Se dice que la función de hash será perfecta si es inyectiva, quiere decir, que para cada dato de entrada se obtiene una cadena diferente. Para que esto ocurra, es necesario que la cardinalidad del conjunto dominio sea inferior o igual a la cardinalidad del conjunto imagen. Normalmente, sólo se dan funciones hash perfectas cuando las entradas están preestablecidas.
Las funciones hash, además de para identificar claves, pueden utilizarse para comparar ficheros. Por ejemplo, la función hash puede leer los primeros párrafos de un fichero y asociarles, similarmente, cadenas alfanuméricas. Si obtenemos la misma cadena, podemos estar casi seguros de que los ficheros son idénticos. ¿Por qué decimos casi idénticos? El físico Bartolo Luque, profesor de la Universidad Politécnica de Madrid, nos explica muy claramente la precisión de las funciones hash en su artículo “El problema del cumpleaños y la seguridad de nuestras contraseñas”, publicado en la revista “Investigación y ciencia” . A continuación resumiremos su explicación e invitamos a leer el artículo completo, mucho más detallado que esta breve entrada en seguridad y criptografía.
Luque menciona “casi” porque existe la posibilidad de que se produzca una colisión. Un tipo particular de función hash produce ristras de 160 caracteres de longitud. Estas secuencias pueden representarse en el sistema hexadecimal, con base 16. Así, nuestra información es capaz de proporcionar 2160=1048 salidas. Además, pueden usarse mensajes con un tamaño máximo de 264 bits, de modo que el número total de argumentos posibles es 103x 10^18, un número inmenso. El número de entradas es inmensamente mayor que el número de salidas, lo que sugiere que muchas entradas generarán el mismo resultado.
Un pequeño cálculo, volviendo al problema del párrafo inicial, nos da que para obtener una colisión con probabilidad ½, aplicando la aproximación de [1,N=1048], obtendremos n=1.18 x 1024 números aleatorios generables en el intervalo.
Como vemos, la función hash goza de una inyectividad lo suficientemente fiable como para que numerosas páginas web cifren con ellas sus bases de datos. Para un pirata informático sería una tarea ardua el descifrar nuestras contraseñas, pues les exigiría encontrar todas las entradas que produjeran un mismo hash o mensaje.
______
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU) y Cristina Sardón (ICMAT-CSIC).
