La solución al desafío áureo de Ciencia descarriada

Este es el desafío áureo. Si no sabés de qué se trata podés consultar primero esta entrada anterior de Ciencia descarriada: El desafío áureo

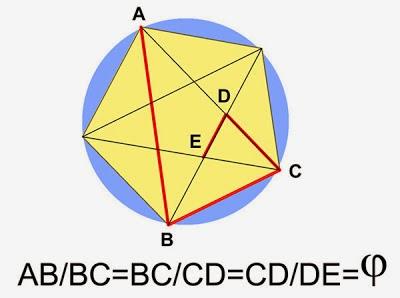
Y ahora sí, a demostrarlo. Vamos, dale, no te inhibas. Es más simple de lo que parece
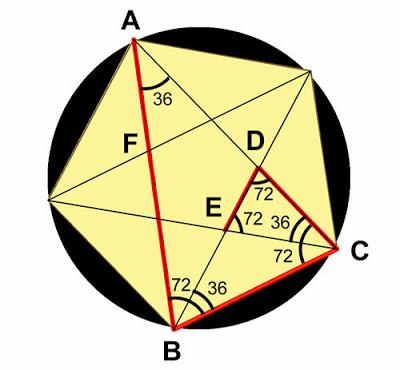
1 - Indiquemos en la figura algunos ángulos.
¿Cómo se calculan? Deducilos vos, es muy fácil!

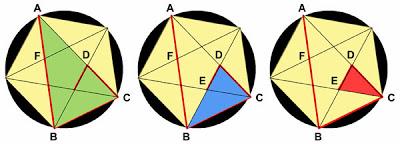
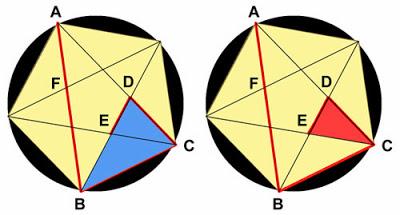
2 - Ahora, con ayuda de las simetrías y los ángulos vemos con claridad tres triángulos isósceles y semejantes, en color verde, azul y rojo

Entonces se pueden hacer estas proporciones.
Primero entre el verde y el azul. El lado del verde es al lado del azul como la base del verde es a la base del azul:
AB/BC=BC/CD (1)

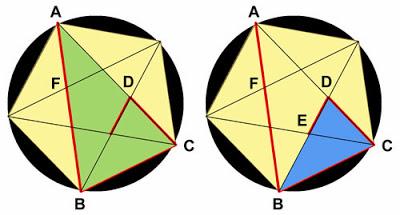
Y ahora entre el azul y el rojo. El lado del azul es al lado del rojo como la base del azul es a la base del rojo:
BC/CD=CD/DE (2)

Por propiedad transitiva, de (1) y (2) nos queda
AB/BC=BC/CD=CD/DE (3)
NO te rindas! Solo falta demostrar que esas tres proporciones son iguales a la razón áurea
3 - Ahora todo está en manos del segmento AB

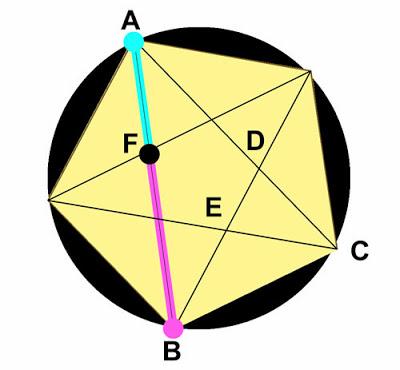
Por definición del número áureo (consultá la entrada El desafío áureo), si en el segmento AB se cumple AB/BF=BF/FA entonces AB/BF=BF/FA=1,618...  ¿Lo demostramos?
Veamos primero a qué es igual AB/BF:
AB/BF=AB/BC, pero de (1): AB/BC=BC/CD, por lo tanto por propiedad transitiva AB/BF=BC/CD (4)
Ahora veamos a qué es igual BF/FA:
Por semejanza de triángulos  BF/FA=BC/CD (5)
Y ahora por propiedad transitiva, de (4) y (5) nos queda que se cumple el planteo inicial AB/BF=BF/FA:
Por lo tanto AB/BF=BF/FA=BC/CD=1,618... (6)
Y de (3) y de (6):  AB/BC=BC/CD=CD/DE=1,618...