La vida es caótica

“It does not say in the Bible that all laws of nature are expressible linearly.”

- Enrico Fermi.

Un personaje clave en la historia de la dinámica de poblaciones es Robert May, cuyo nombre completo era Robert McCredie May.

Robert May

May nació en la ciudad australiana de Sydney, el 8 de enero de 1838, y asistió a una escuela local. Su infancia fue solitaria, dedicada a resolver rompecabezas y juegos, aunque llegó a ser un auténtico campeón en los típicos debates de las escuelas británicas. Sus estudios universitarios de ingeniería química los hizo en la Universidad de Sydney, donde además estudió matemáticas y física teórica, disciplina esta última en la que realizó su tesis doctoral en 1959, sobre superconductividad. Su formación multidisciplinar fue sin duda clave para su investigación posterior.

Al terminar su tesis, May consigue un contrato postdoctoral en la Universidad de Harvard, como profesor Gordon MacKay, en matemática aplicada. A finales de 1961, vuelve a Sydney donde desarrolla su carrera investigadora en su Departamento de Física hasta 1973. Comienza a interesarse por la dinámica de poblaciones, especialmente en una estancia de año y medio en el Reino Unido y en Princeton. En 1973 acepta un puesto de catedrático en Princeton, en el Departamento de Biología, trasladándose una vez más, en 1988 a la Universidad de Oxford, como profesor de la Royal Society, de la que será presidente desde 2000 a 2005. Actualmente es profesor emérito de Oxford.

Una reflexión sobre esta intensa vida académica señala diferencias fundamentales con el sistema universitario español, no sólo por el cambio de universidades, sino sobre todo por el cambio de temáticas y de departamentos tan dispares: Matemática Aplicada, Física, Biología.

A lo largo de su vida Robert May realizó investigaciones muy diversas, pero nos vamos a centrar aquí en sus trabajos sobre dinámica de poblaciones. Si r es la tasa de crecimiento, se tiene

x_n+1 = r x_n

y si suponemos que

r(x) = r (1-x)

obtenemos la ecuación logística

x_n+1 = r x_n(1 − x_n)

Podemos por ejemplo pensar en la población de insectos de una isla que va creciendo con tasa r pero que, como las fuentes de alimentación disminuyen, también lo hará la tasa de fertilidad.

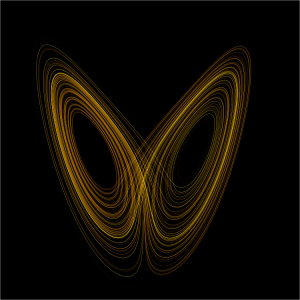
El atractor de Lorenz

La teoría del caos toma cuerpo a comienzos de los años 60 del siglo pasado, cuando Edward Lorenz, trabajando con unas ecuaciones, dejó el lento ordenador de entonces trabajando y se tomó un descanso. A su vuelta se encontró con una figura que ahora se conoce como atractor de Lorenz. Lo que Lorenz entendió es que en su simulación, cambios pequeños en las condiciones iniciales producían cambio muy grandes con el paso del tiempo, esta es la característica de los sistemas caóticos. El resultado fue publicado en un famoso artículo, Deterministic Nonperiodic Flow (Flujo determinista no periódico). Journal of Atmospheric Sciences. Vol.20, (1963), 130-141. Posteriormente, en la reunión anual de 1972 de la American Association for the Advancement of Science (AAAS), en el MIT, presentó una ponencia con el título: Predictability; Does the Flap of a Butterfly’s wings in Brazil Set Off a Tornado in Texas?, (Predictibilidad, ¿El aleteo de una mariposa en Brasil puede producir un tornado en Texas?), de donde nació el término de efecto mariposa.

Una década después del descubrimiento de Lorenz, Robert May hizo un descubrimiento similar, con tremendas consecuencias para la biología. Considerando la función

F(x) = r x (1-x)

descubrió que el comportamiento del correspondiente sistema dinámico era extremedamente complejo según los valores de r.

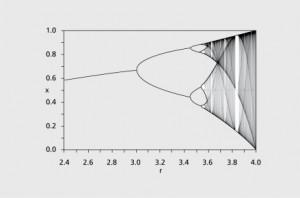
En su artículo Simple mathematical models with very complicated dynamics, publicado en Nature en 1976, escribe:

” . . . the very simplest nonlinear difference equations can possess an extraordinarily rich spectrum of dynamical behaviour, from stable points, through cascades of stable cycles, to a regime in which the behaviour (although fully deterministic) is in many respects ”chaotic”, or indistinguishable from the sample function of a random process.”

Este comportamiento se reflja en la gráfica que incluimos unas líneas más arriba.

Robert May ha recibido muchísimos honores, entre ellos, una baronía, de manera que ya es un Lord. Aparte de su asesoramiento al gobierno británico en cuestione scientíficas, continúa trabajando en  biología matemática, en problemas de medioambiente, biodeversidad, etc. Sus conocimientos de matemáticas le han permitido obtener nuevos resultados sobre las distribuciones de virus y bacterias, en inmunología a enfermedades transmitidas por parásitos, en avances contra el SIDA, pero también en el análisis de la biodiversidad en regiones tropicales. En este último campo, la combinación de matemáticas, biología y computación, le han permitido obtener avances sobre como prevenir un colapso de la biodiversidad.

Les dejamos aquí con un ainteresante charla de Robert May en Cambridge, What does the future hold?

____

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU).

Guardar

Guardar

Guardar

Guardar