Antes que nada, gracias a todos los que participaron ayer en los comentarios resolviendo los 5 ejercicios. El nivel ha sido de gran calidad y eso tiene su mérito en los tiempos que corren. Os decía ayer que iba a hacer unas comparaciones con el libro “Matemáticas I” de la editorial Santillana, Serie Resuelve.
La lección sobre inecuaciones lineales de primer grado (recordad que una ecuación de primer grado siempre es lineal, a diferencia de las de segundo grado que son cuadráticas y se dibuja en forma parabólica) con una incógnita la encontramos en la página 50 del libro citado. Como viene siendo habitual en los libros de textos modernos, aunque parezca difícil de creer, la editorial Santillana solo le dedica UNA página (en realidad, una mitad de la página) a exponer qué es una inecuación de primer grado con una incógnita. Voy a copiar exáctamente lo que dice el libro y entonces entraré en la lección magistral de hoy.
Cito textualmente y los siguientes ejercicios son, repito, de la página 50.
“Una inecuación es una desigualdad que se compone de dos expresiones algebraicas separadas por uno de estos signos:
, ≤, o ≥
Su solución está formada por todos los valores que hacen que sea cierta la desigualdad numérica.”
EJEMPLO:
Determina si x = 2 y x = -3 son soluciones de estas inecuaciones:
2x – 1 > 2
2 x 2 – 1 > asi que x = 2 es solución de la inecuación.
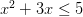
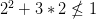
El caso de -3 NO es solucion en la primera inecuación, pero sí en la segunda.
Así es como lo explica el libro de Santillana, ¡¡sin más!!
Unos apuntes más de Santillana. Dice:
“Si multiplicamos una desigualdad por un número negativo, el signo de la desigualdad cambia.
2x ≤ 2
-1 * (2x) ≥ -1 * 2
Si en la inecuacion la desigualdad es ≤ o ≥, el extremo común de los intervalos siempre pertenece a la solución.
Dan un ejemplo más y entonces unos ejercicios sencillitos. El ejemplo es el siguiente:
Resuelve la inecuación con una incógnita
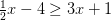
PRIMERO. Se agrupan los términos con x en un miembro y los independientes en el otro miembro.
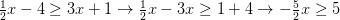
SEGUNDO. Se despeja la variable x, teniendo en cuenta que si el coeficiente de la variable x es negativo, al despejar la desigualdad cambia de signo.
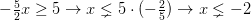
TERCERO. Se escribe la solución de la inecuación.
$latex \{X: -\infty 7. Esta inecuación nos dice que x es mayor a 7. Es decir, x puede ser 8, 9, etc pero por supuesto NO puede ser -5. Podemos ver la solución a esto de forma gráfica tal y como podéis ver en la siguiente recta numérica:
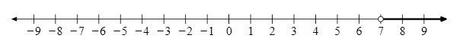
Dibujamos un círculo abierto en x = 7 para dejar claro que 7 NO ES UNA SOLUCIÓN a la inecuación porque obviamente 7 NO es mayor que 7…a no ser que vivas en un mundo paralelo donde te inventas las normas como te da la gana, pero si eres de ese tipo de persona, mejor ya ve cerrando la página porque este no es tu sitio ni tu mundo. La parte negrita en la recta indica TODAS las soluciones posibles a la inecuación.
Al igual que utilizamos círculos abiertos para marcar los puntos finales de una desigualdad ESTRICTA como es x > 7, utilizamos círculos cerrados para marcar una desigualdad NO estricta como por ejemplo sería
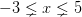
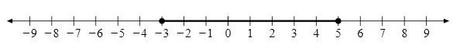
Los círculos cerrados en los puntos -3 y 5 indican que estos números SÍ son soluciones válidas.
Las soluciones a los problemas de inecuaciones deberían ser escritos utilizando la NOTACIÓN DE INTERVALOS. Por ejemplo, podemos utilizar la notación para escribir “todos los números igual o mayores a -3 e igual o menos que 5” utilizando el intervalo: [-3,5]. Nótese que siempre escribimos la solución más inferior primero. En este caso, -3. No sería correcto escribir [5, -3].
Usar esta notación para indicar que
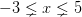
![x\in[-3,5] x\in[-3,5]](https://m1.paperblog.com/i/595/5957280/inecuaciones-lineales-clase-magistral-L-Y3hanR.png)
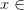
Para excluir un valor límite de un intervalo, utilizamos “(” para el límite inferior y “)” para el límite superior. Por ejemplo, la declaración matemática
![x\in(-3,5] x\in(-3,5]](https://m1.paperblog.com/i/595/5957280/inecuaciones-lineales-clase-magistral-L-EiOO_O.png)
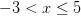
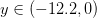
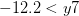
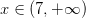
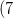
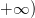
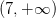
![w \in (-\infty,-2] w \in (-\infty,-2]](https://m1.paperblog.com/i/595/5957280/inecuaciones-lineales-clase-magistral-L-8v2MEY.png)
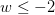

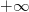
Varios ejemplos:
EJEMPLO 1:
¿Cuáles son todos los valores de x que satisfacen
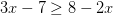
SOLUCIÓN:
Sumamos 2x a los dos lados para arrejuntar todos los términos con x en el mismo lado…que en las matemáticas nos gusta lo que es igual, junto.
Ahora tenemos lo siguiente:
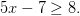
Ahora debemos sumar 7 a los dos lados para seguir en nuestro proceso de aislamiento.
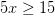
Hay que simplificar esto dividiendo por 5 para reducir la fracción. Finalmente:
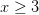
Podemos escribir esta solución utilizando la notación de intervalos:
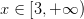
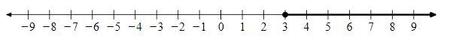
EJEMPLO 2:
Resolver las siguientes inecuaciones de primer grado:
(a)
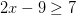
(b)
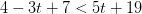
SOLUCIONES:
(a) Sumando 9 a los dos lados nos da
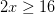
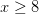
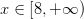
(b) Se puede simplificar el lado izquierdo y esto nos da
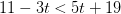
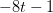
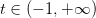
EJEMPLO 3:
Resuelva la siguiente cadena de desigualdades:
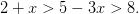
¡Anda! Pues no podemos hacerle frente a toda la cadena a la vez, porque si restamos x de TODAS las 3 partes para eliminar x al extremo izquierdo, entonces tendremos una x a la extrema derecha de la cadena. Me temo que esto va a ser como lo que pasa con los hombres que se enrollan en líos con más de una mujer. Se tendrá que lidiar con las dos de forma separada.
Primero, tenemos
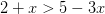
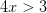
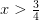
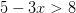
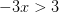
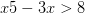
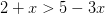
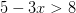
Las soluciones entonces son
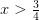
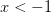
EJEMPLO 4:
Estoy pensando en un número. Tres más que el doble de mi número is menos que 17, pero al menos -1. Si mi número es un número entero, ¿cuáles son los valores posibles?
SOLUCIÓN:
Llamemos mi número “n”. La inecuación algebraica de lo que yo he dicho verbalmente arriba es
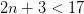
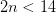
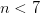
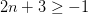
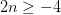
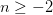
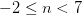
Ya que mi número debe ser un número entero, los valores posibles son: -2, -1, 0, 1, 2, 3, 4, 5, y 6.
Nótese que hacemos las mismas manipulaciones cuando resolvemos ambas desigualdades: restamos 3, dividimos por 2. De hecho, podríamos habernos enfrentado a las dos desigualdades a la vez mediante una cadena de desigualdades. La información dada al principio puede representarse con la siguiente cadena:
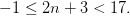
Restando 3 de los dos lados y tenemos:
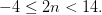
Dividiendo las dos partes por 2, nos queda:
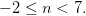
A ver si podemos utilizar esta táctica de "dos a la vez" (una orgía matemática) en el siguiente ejemplo:
EJEMPLO 5:
¿Qué valores de "x" es la cantidad
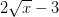
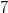
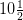
Empezamos por "traducir" la expresión verbal en una declaración matemática:
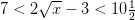
En realidad, hacemos lo mismo que si esto fuera una ecuación lineal "disfrazada" de otra cosa.
Podemos aislar el término
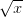
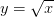
Sumamos 3 a los dos lados.
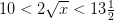
Entonces dividimos por 2 y nos da como resultado:
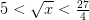
Seguimos sin haber aislado la x. Sin embargo, x tiene que ser claramente POSITIVA y también lo son 5 y 27/4. Podemos elevar al cuadrado los dos lados de esta cadena sin cambiar los símbolos de las desigualdades:
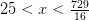
Escribimos la solución final en notación de intervalos (a mis alumnos les resto puntos si no me lo ponen en la notación exigida, ya que la falta de formalidad es una forma de faltar al respeto a la logica):
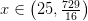
Bien, ya hemos terminado la clase magistral por ahora. ¿Notais diferencias entre el tratamiento que le da Santillana al que le damos aquí? Los siguientes son ejercicios para los señores de ayer que dieron la talla. A ver si la pueden dar con los siguientes:
————————————————————–
1) A finales de enero del 2003, la población de mi pueblo era 11.212. La población de mi pueblo aumenta en 322 personas cada mes. ¿En qué mes por primera vez la población de mi pueblo supera los 15.000 habitantes?
2) ¿Cuál sería la longitud del intervalo de las soluciones para la inecuación siguiente?
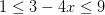
3) Determina la cantidad de números positivos enteros que puedan satisfacer la siguiente inecuación. ¿Existe algún número entero negativo que también pueda satisfacerla?
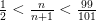
4) ¿Cuál sería el número entero "K" más grande que cabría en la siguiente inecuación?
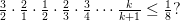
———————
UN APUNTE FINAL MUY INTERESANTE:
El "infinito" es un concepto difícil de definir. Hablando muy a la "barra de bar", cuando utilizamos la infinidad en las matemáticas, estamos hablando de un número que es más grande que cualquier número específico que se te ocurra. La infinidad es el resultado del hecho que NO existe "el número más grande". Si pensáramos que un número fuese el más grande posible, entonces siempre podríamos sumarle 1 y tener un número mayor.
La idea del infinito ha provocado problemas en muchos matemáticos y filósofos. Por ejemplo, el filósofo griego Zenón de Elea, creó varias paradojas, una que dice algo como lo siguiente:
Suponiendo que quieres cruzar la calle. Para alcanzar el otro lado, debes ir a la mitad del camino cruzando la calle. Pero antes, debes caminar la mitad al punto que esté a la mitad del camino al cruzar la calle. Pero es que incluso antes de hacer esto, debes caminar la mitad a un punto que esté a un cuarto del camino al cruzar la calle. Ya que hay una infinidad de pasos, ¡¡no existe el movimiento!!
No descartes esta paradoja como una tontería. Es una cuestión fundamentalísima y clave en muchas cosas de las matemáticas sofisticadas.
