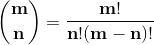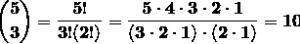Las maravillosas propiedades del triángulo de Pascal

Una de las herramientas mágicas de las matemáticas es el triángulo de Pascal. Además de ser muy útil, también es muy sencillo de construir. Incluso puede ayudarte en algún examen y en la vida real. ¿No te lo crees? Compruébalo tu mismo.

Triángulo de Pascal, de Tartaglia o numérico

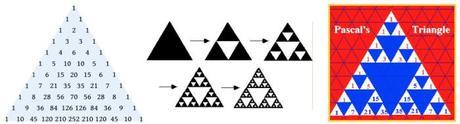
Así me llaman, aunque no soy un triángulo geométrico, más bien una disposición numérica en forma de triángulo. Soy una figura elegante, repleta de muchas características interesantes.

Cada linea se construye a partir de la anterior. Con excepción de los números 1, que siempre están en los extremos, cada número es igual a la suma de los dos números que tiene por encima.

Las aplicaciones del famoso triángulo ya las conocían los matemáticos indios (siglo XI), chinos y persas. Pero fue el filósofo y matemático francés Blaise Pascal (1623-1662) el primero en organizar muchas propiedades de manera conjunta, escribiendo el primer tratado sobre esta disposición numérica.

En Italia todos lo conocen como el triángulo de Tartaglia, en honor al algebrista italiano, unos de los principales matemáticos del siglo XVI y seguramente el primero en publicarlo en Europa.

Infinito y simétrico

No tiene fin y es simétrico respecto al eje vertical. Se puede leer igualmente empezado por la izquierda que por la derecha.

Potencias cuadradas

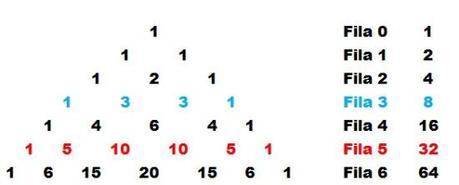
La suma de todos los valores de cualquier fila del triángulo, es igual a una potencia de 2. La primera fila se denomina fila cero.

De esta forma se obtienen todas las potencias de 2:  1,2,4,8,16,32,64,128,256, etc.

Potencia de una suma

Observa con atención y verás cómo cada fila del triángulo de Pascal corresponde a los coeficientes del desarrollo de la potencia de un binomio

Esta propiedad es muy utilizada en matemáticas. Es uno de los errores típicos de álgebra que cometen los estudiantes. Conociendo este triángulo numérico, es difícil que te equivoques.

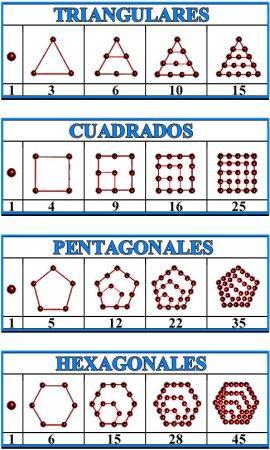
Números poligonales

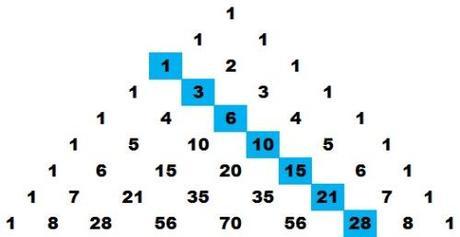
Fueron descubiertos por los pitagóricos. Están presentes aquí, absolutamente todos los que quieras tener. ¿Los encuentras? Te echo una mano. En la diagonal pintada de color azul, se encuentran los números triangulares.

Los números cuadrados están un poco “más escondidos”.  Coge esta misma diagonal y haz una pequeña operación para obtenerlos:

1        1+3=4        3+6=9       6+10=16     10+15=25       15+21=36       21+28=49     etc.

Como ves cada número cuadrado se obtiene sumando dos números triangulares consecutivos. Tiene su lógica, porque un cuadrado es la suma de dos triángulos.

Números pentagonales

En este caso tienes que coger la diagonal de los números naturales.

1        2+3=5      3+4+5=12        4+5+6+7=22       5+6+7+8+9=35      etc.

Observa el patrón numérico que se cumple, realmente bonito.

Números hexagonales

Estos se ven a simple vista. ¿Ya los tienes? Van dando saltos. Sí, también aparecen en la diagonal coloreada de azul.

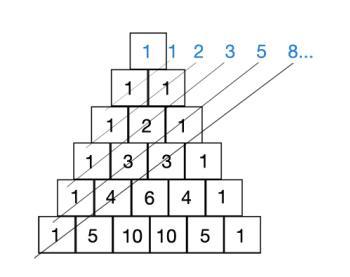
Sucesión de Fibonacci

Seguramente habrás oído hablar de ella. También la encontramos en este conjunto mágico de números.

¿Qué pasará si diferenciamos los números pares de los impares? 

Al usar diferentes colores para distinguirlos, obtenemos … un fractal !! A ver quien me dice ahora que las matemáticas son aburridas …

Obtenemos un patrón igualito al triángulo de Sierpinski. Si quieres profundizar un poco en relación a los patrones que pueden formarse en el triángulo de Pascal, puedes entrar aquí.

Puedes construir fácilmente este fractal a partir de un triángulo equilátero (hazlo bien grande). Une los puntos medios de los lados y obtendrás 4 triángulos. Uno en el centro invertido. Después tienes que ir repitiendo el proceso en cada uno de los triángulos que se apoyan en su base.

Un  objeto con estas características de auto semejanza en distintas escalas, se denomina fractal. Podemos decir entonces que el triángulo de Pascal es un fractal, aunque bien es verdad que hay que buscarlo. ¡qué importante es dibujar en matemáticas!

Te permite calcular probabilidades

♣ ¿Cuál es la probabilidad exacta de sacar exactamente dos caras tirando cuatro monedas?

Tengo 4 objetos, me voy a la fila 4. Observo que tengo 16 casos posibles (sumando los valores de esa fila)

Tengo que sacar 2 caras. Cuento hasta llegar a la casilla número 2 de esta fila (el primer 1 es la posición cero). Obtengo el número 16.

  6/16= 37’5%

♠ ¿Cuál es la probabilidad de obtener tres caras tirando cinco monedas?

¿Te sale que es igual a un 31’25%? Estupendo!!

Imagínate la cantidad de apuestas que puedes hacer con tus amigos. Cuestión de probabilidades …

… y posibles combinaciones de elementos

Los números del triángulo de Pascal coinciden exactamente con los números combinatorios.

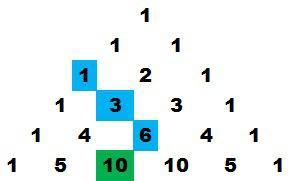
Por ejemplo, si tienes cinco libros, ¿de cuántas maneras puedes elegir tres libros para leer durante unas vacaciones (no importa el orden)?  

Ves a la fila 5 , y sitúate en la posición número 3 (recuerda que el primer 1 es la posición cero). Esa es la respuesta! De 10 formas diferentes.

Potencias de 11

También están todas. Sólo tienes que “ver” cada fila como un único número. A partir de la quinta fila, cuando ya aparecen números de 2 cifras, necesitamos agrupar estos números para obtener la potencia de 11

Actividades

A continuación, te propongo una serie de actividades recreativas para que te des cuenta de las grandes relaciones que esconde este triángulo mágico.

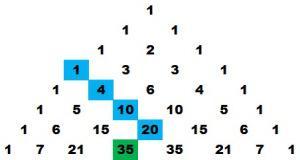
En los siguientes diagramas hay una relación entre los números azules y el número de color verde. ¿Puedes verla?

       

La encontraste, ¿verdad? Observa que el patrón de esta relación se cumple siempre en cualquier parte del triángulo numérico.

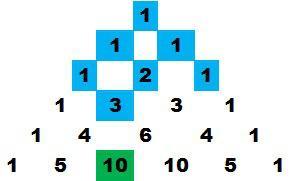
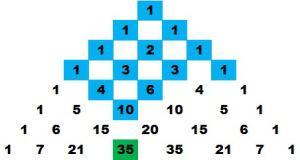
La siguiente también es sencilla. ¿Puedes encontrarla? ¿Eres capaz de enunciar dicha relación?

 

Como ves las posibilidades que ofrece el triángulo de Pascal son enormes. Permite resolver muchos problemas de cálculo. Te aseguro que aprenderás mucho si sigues descubriéndolas por ti mismo. Dale rienda suelta a tu imaginación y disfruta jugando con los números, las matemáticas no te decepcionarán …

Te espero en los comentarios de tu blog de matemáticas. Si te ha gustado el artículo, compártelo en tus redes sociales.

Fuentes 1 2     Imágenes 1 3 5 6 7 8 9