Las matemáticas del Carbono 14

¿Es la Sábana Santa la tela de lino que se expone en la Catedral de Turín? ¿De qué fecha datan algunas de las pinturas rupestres más importantes de Europa? Éstas y otras preguntas son, hoy en día, fáciles de responder gracias a la técnica de datación por radiocarbono, más conocida como técnica del Carbono 14. Tras esas técnicas se esconde un sencillo modelo matemático que, en gran medida, es el responsable de todo esto. Vamos a hablar hoy de todo esto.
Antes de continuar, quiero advertir a todos de una cosa. Yo soy matemático, no químico, por lo tanto los detalles de esta última rama van a ser simplificados, eso sí, intentando no perder el rigor necesario. Si algún Químico piensa (César, por favor, no me lo tenags en cuenta) que debo rectificar algo, os dejo los comentarios para ello. Y sobre todo: perdonadme.
Ahora sí. Comencemos hablando de radiación y de su modelo matemático. En 1902 Ernest Rutherford y Frederick Soddy, quienes en 1908 y 1921 respectivamente fueron galardonados con el Premio Nobel de Química, estudiaron la desintegración de la materia por emisión de radiactividad. Las observaciones experimentales que realizaron les llevaron a proponer que la cantidad de núcleos atómicos 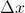de una sustancia radiactiva que se desintegran en un intervalo de tiempo 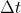es directamente proporcional al número de núcleos presentes, 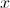, y al intervalo 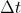. Es decir, 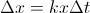para cierta constante de proporcionalidad 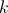. Si tomamos intervalos de tiempo infinitesimales, o equivalentemente, si hacemos que , obtendremos una ecuación diferencial que modeliza el comportamiento de estos átomos 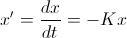donde el signo menos es debido a la disminución de la sustancia y 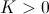es la conocida como constante de desintegración del elemento radiactivo.
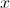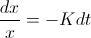La ecuación que define el modelo de desintegración radiactiva es de variables separables, por lo que si procedemos a romper la diferencial y separar la de la , obtenemos que , por lo que al integrar se convierte en 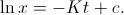Si llamamos 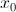a la cantidad de sustancia radiactiva que se tenía en el instante inicial 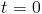, obtenemos una condición inicial del problema 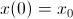con la que es fácil determinar que la constante de integración resulta ser 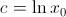, de modo que la solución será 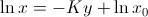que al despejar resulta .
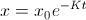Habitualmente, la constante de desintegración radiactiva se expresa a través de lo que se conoce como vida media de la sustancia, es decir, el tiempo necesario para que una cierta cantidad dada se reduzca a la mitad. Para calcular esta vida media, que denotaremos por 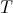, basta tomar 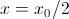y 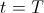, es decir, 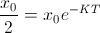, de donde 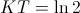y la solución resulta .
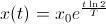¿Y qué tiene que ver esto con el Carbono 14? Pues mucho. Resulta que el Carbono-14 es un isótopo radiactivo del Carbono. Más o menos queire decir que se trata de un compuesto inestable que por radiación pasa a convertirse en Nitrógeno-14, que ya sí que es estable. Resulta que en la atmósfera convicen hasta 3 isótopos del Carbono: Carbono-12, Carbono-13 y Carbono-14 (los dos primeros estables y el último, como ya hemos dicho, no). Sin embargo el Carbono-14 se genera de forma espontánea en la atmósfera debido al continuo bombardeo de neutrones que absorben los átomos de nitrógeno. El proceso de generación (por bombardeo) y degeneración (por radiación) provoca que la cantidad de Carbono-14 en la atmósfera con respecto al Carbono-12, permanezca constante.
Vale, en la atmósfera es constante, ¿y qué? Pues que como las plantas utilizan ese carbono para la fotosíntesis, asimilan la misma cantidad de Carbono-14 de la atmósfera... y los seres vivos que se nutren de las plantas también lo asimilan. Y todo esto ocurre hasta el preciso momento en que el ser vivo muere: entonces (en el ser vivo ya muerto) se detiene el proceso de creación de Carbono-14 (ya no se ingiere más) y sólo queda el proceso de degeneración, por lo que la radiactividad sigue su curso, y su curso es una Ecuación Diferencial.
Por tanto, basta calcular la cantidad de Carbono-14 que queda en la materia orgánica (bueno, el cociente de esta cantidad respecto del Carbono-12) que queramos datar, aplicar la fórmula 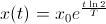y tener en cuenta que, en este caso, 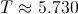años. Esta datación se conoce como Edad Radiológica.
Bueno, las cosas no son exactamente tan sencillas, pues a lo largo del tiempo se sabe que la cantidad de Carbono-14 en la atmósfera ha ido variando, por lo que en realidad, puede que los resultados obtenidos se alejen un poco de la realidad. Afortunadamente, hemos sido capaces de conocer con cierta precisión la evolución de la presencia de Carbono-14 en la atmósfera en los últimos 15.000 años, por lo que ahora, basta tabular la evolución (se suele hacer en forma de curva) tomar la Edad Radiológica y rectificarla según esos datos.
Bueno, ya poco más queda por decir. Sólo que para los cálculos, suele utilizarse como año de referencia 1950, por convenio y más que nada porque las pruebas nucleares que se efectuaron poco después hicieron que esas curvas de radiactividad sufrieran picos inesperados que complicarían las cosas. Así que datamos desde 1950 hacia atrás y desde entonces hasta ahora, sólo hay que sumar.
Resumiendo, las Ecuaciones Diferenciales al servicio, en este caso, de la química. Además, hay otras técnicas de datación que se basan en el mismo principio, como la que se utiliza para datar granitos. En estos casos el elemento radiactivo es el Uranio, que se descompone, trasd varias fases en Helio y Plomo con una vida media de 4500 millones de años.
Tito Eliatron Dixit
PD: Esta entrada forma parte de la IX edición del Carnaval de Química que se celebra en el blog Hablando de Ciencia. 
 
Si te ha gustado esta entrada, puedes dejar un comentario directamente en Tito Eliatron Dixit.
 
O votarme en los premios Bitacoras 2011: