Las matemáticas más sencillas de la dinámica de poblaciones

Las Matemáticas, a pesar de ser probablemente la disciplina más odiada, se ha revelado capaz de modelizar prácticamente cualquier situación que las ciencias experimentales se plantean. En las siguientes líneas vamos a centrarnos en unos modelos sencillos de dinámica de poblaciones de una única especie, los modelos malthusianos y logísticos, y en las sencillas matemáticas que éstos implican: las ecuaciones diferenciales de variables separadas.
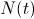Establezcamos unas sencillas bases de trabajo. Supongamos que tenemos una especie sobre la que queremos estudiar el número de individuos. En un instante de tiempo, habrá individuos. Ya que estamos suponiendo, pongamos que tenemos muchísimos individuos... tantos que no nos importará suponer que 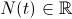y que la función 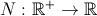es continua y, ya que estamos, derivable. Os recuerdo que estamos modelizando, esto se tiene que parecer a la realidad, no ser exactamente igual a la realidad: digamos que lo que pretendemos es un primer acercamiento a la realidad.
El crecimiento de la población entre dos instantes 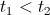diferentes será ; mientras que la tasa de crecimiento será 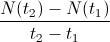. Al igual que con las velocidades en física, si queremos una tasa instantánea de crecimineto o velocidad de crecimiento, basta hacer que 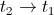y así obtenemos 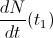. O dicho de otra forma, la derivada (que para eso hemos supuesto que 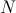es derivable) 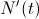de la función de población 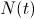, mide la velocidad con que la especie crece o decrece.
Comencemos pues, con el modelo malthusiano. En éste, se supone que la tasa de variación depende única y exclusivamente de los nacimientos y las defunciones y, además, que éstos son proporcionales al número de individuos de la población. Es decir, se supone que 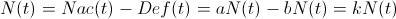, Así pues, hemos llegado a una ecuación diferencial: 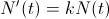, o lo que es lo mismo, 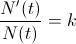lo que nos sugiere que 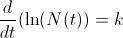, de donde 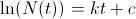y, finalmente, obtenemos que 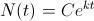. Si ahora suponemos que conocemos el número de individuos al comienzo de nuetras indagaciones, pongamos 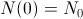, es claro, pues que la solución al modelo malthusiano es .
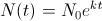La consecuencia de esto es, por un lado, lo que en su día (allá por 1800) propuso Malthus. Si 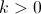, es decir, si hay más nacimientos que muertes, entonces la población de esta especie crecería exponencialmente; por otro lado, si 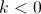, es decir, si hay más defunciones que nacimientos, resulta que la población decrecerá (también exponencialmente) hasta llegar a desaparecer (técnicamente, nunca sería 0, pero como estamos hablando de cantidades discretas que hemos supeusto continuas, podemos decir que para valores muy pequeños, no quedarán individuos); finalmente, si 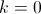es decir, si los nacimientos y las muertes son las mismas, la población quedaría estacionaria en 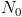individuos.
Evidentemente, esta modelización es un inicio, pero para nada describe lo que suele ocurrir en general. En cualquier caso, se suele utilizar para intervalos cortos de tiempo, y se ha usado para el estudio de colonias de bacterias, poblaciones de pequeños mamíferos e incluso
para población humana.
El modelo anterior presenta unas carencias evidentes, y es que omite factores importantes (migraciones, relaciones entre individuos...). En 1836 Pierre François Verhulst propone una alternativa a este modelo básico en el que vamos a centrarnos, el modelo logístico.
El modelo logístico se basa en el malthusiano, pero incluye, además, la competencia entre los individuos de la especie como factor que influye en los nacimientos y las muertes (bien por la lucha por alimentos, bien por la supervivencia ante enfermedades u otra razón diferente). Verhulst supuso razonable pensar que este factor sea proporcional a la cantidad de interacciones que pueda haber entre individuos de la especie. Si tenemos 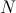individuos, el número de posibles contactos (esto no es más que el problema de los apretones de manos) será 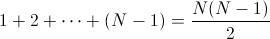. Así la ecuación logística será de la forma
.
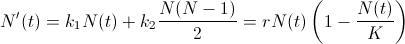Las constantes que aparecen, tienen un significado importante. La constante 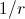, que está en escala temporal, proporciona el intervalo de tiempo en el cual el modelo puede considerarse como una aproximación aceptable al problema real; mientras que 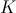recibe el nombre de población límite (veremos ahora la razón).
Pues bien, esta ecuación también es de variables separadas y no es complicada de resolver. Basta escribirla de la siguiente forma (poniendo 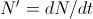): 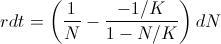, de donde es fácil concluir que 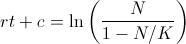. Parémonos aquí un momento y, al igual que en el modelo malthusiano, impongamos que para 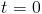, conocemos que 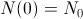. Así, es fácil calcular la constante de integración 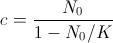. Ahora ya sólo queda tomar logaritmos y sustituir el valor de para llegar a la Ecuación Logística: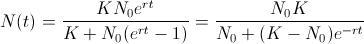
.
Como ya indicamos, la constante 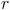es de tipo temporal, por lo que la asumimos positiva. En estas condiciones, en función de 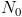y 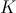tendremos un comportamiento u otro. En concreto, si 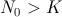habrá decrecimiento sin bajar del límite poblacional 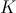; si 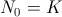la población permanece constante; si 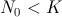habrá crecimiento sin sobrepasar el límite poblacional 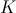, pero el comportamiento difiere ligeramente si 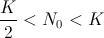o bien si 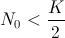, como podréis comprobar en el dibujo
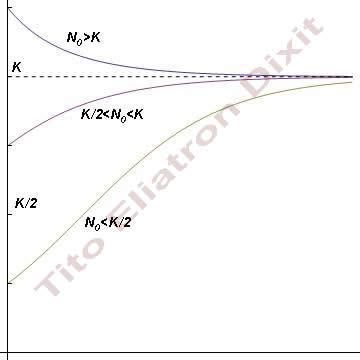Lo que se conoce como curva logística, se parece más al último comportamiento, es decir, cuando 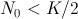, en donde se observa al principio un crecimiento rápido para pasar (a través de un punto de inflexión de la curva) a un crecimiento más atenuado para no llegar a sobrepasar el límite .
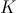Como habéis podido ver, son modelos extremadamente sencillos en los que intervienen pocos factores, por lo que no siempre se ajustan a la realidad. Hay otros muchos modelos, más complejos e intrincados, pero cuya resolución ya no es tan sencilla como estos. Los dejaremos para futuras entradas.
PD1: Esta entrada forma parte de la Edición 2.2 del Carnaval de Matemáticas cuyo anfitrión, en este mes, es Gaussianos.
PD2: Esta entrada forma parte del II Carnaval de Biología cuyo anfitrión es La muerte de un ácaro.
Tito Eliatron Dixit

---

Referencias:
Modelos Matemáticos basados en E.D.O. de Primer Orden I , de M.A. González León.
Modelos matemáticos de Poblaciones, de A. Rodríguez Bellido 
 
Si te ha gustado esta entrada, puedes dejar un comentario directamente en Tito Eliatron Dixit.