Los calculadores de Merton

El Merton College albergó a un grupo de estudiosos dedicados al cultivo de la física, la astronomía y las matemáticas, que son conocidos como “los calculadores de Merton”.

Merton College

El Merton College es uno de los colegios de la Universidad de Oxford en Inglaterra. Su fundación se remonta a la década de 1260 cuando Walter de Merton, canciller de Enrique III y más tarde de Eduardo I, redactó por primera vez los estatutos de una comunidad académica independiente y estableció una dotación económica. Es interesante saber que en este colegio las dotaciones se otorgaban directamente al director y a los becarios para que fuera autogobernado sin influencias externas.

Los principales “calculadores”, que escribieron en el segundo cuarto del siglo XIV, fueron Thomas Bradwardine, William Heytesbury, Richard Swineshead y John Dumbleton. Estos “calculadores” dedicaron mucho tiempo al estudio de la mecánica, tratando de encontrar las leyes que determinaban el movimiento de los cuerpos. Al hacerlo, anticiparon muchos desarrollos que después Galileo Galilei e Isaac Newton convirtieron en los resultados que contribuyeron a poner los cimientos de la ciencia moderna, especialmente en física y matemáticas.

Walter Merton

Entre los calculadores, el más destacado sea probablemente Thomas Bradwardine. Nació en Sussex, en 1290 (algunos autores señalan el 1295 o 1300), estudió en el Balliol College, de Oxford, y tras conseguir su título en 1321 pasó a formar parte delMerton College. Allí trabajó hasta 1335, y es en esa época cuando hizo sus contribuciones más relevantes, entre ellas el”Tractatus de proportionibus velocitatum in motibus”. El objetivo de esta obra era encontrar las leyes de la dinámica. Fue confesor del rey Eduardo III y lo acompañó en la guerra en Francia. A su vuelta a Inglaterra, ocupó varios cargos, y en 1349 los canónigos de Canterbury lo eligieron arzobispo, pero Eduardo III prefirió nombrar a su canciller John de Ufford. Ufford murió por la peste y Bradwardine ocupó su lugar, pero cuando volvía de recibir la confirmación del Papa Clemente VI en Aviñón, también sucumbió por la epidemia, sinendo enterrado en Canterbury.

Su influencia fue enorme, convirtiéndose en un célebre teólogo, que llegó a ser conocido como Doctor Profundus. Esa fama le hizo aparecer citado en Los cuentos de Canterbury de Geoffrey Chaucer:

“Con todo, yo no puedo llegaral fondo de la cuestión como aquel santo teólogo San Agustín, Boecio o el obispo Bradwardine y deciros si la divina presciencia de Dios constriñe necesariamente a uno a que realice cualquier acto en particular (cuando indico «necesariamente» quiero decir «sin más» o si uno está en situación de decidir libremente lo que hará o dejará de hacer, incluso cuando Dios sabe por anticipado que el acto en cuestión tendrá lugar antes de que ocurra o si el hecho de que lo sepa no constriñe en absoluto excepto por «necesidad condicional»). En tales problemas no entro en absoluto.”

Hoy sabemos (Newton dixit) que la fuerza que se aplica a un cuerpo le proporciona una aceleración en relación con su masa, es la llamada segunda ley de Newton, fuerza = masa x aceleración. Pero esto no estaba claro en esa época, en la que tampoco se conocía la noción de derivada (de nuevo Newton).

Bradwardine desarrolló sus ideas en el tratado De proportionibus velocitatum in motibus, publicado en 1328. Parece evidente lo que Aristóteles estableciera: el movimiento sólo puede ocurrir cuando las fuerzas que actúan en un cuerpo superan las fuerzas de resistencia. Lo que Bradwardine intentaba dilucidar es cómo la velocidad de un cuerpo en movimiento depende de las fuerzas que actúan sobre él. Así, si V denota la velocidad, F la fuerza motriz y R la fuerza de resistencia, entonces ya Aristóteles decía que V debería ser proporcional al cociente F/R. Supongamos que en principio tenemos una fuerza F fijada, una resistencia R₀ tal que F> R₀  y una velocidad inicial V₀. Si V es proporcional a F/R y las velocidades fueran reduciéndose a la mitad en cada instante de tiempo y, en proporción las fuerzas de resistencia se doblaran, llegaríamos a un momento en que F<R_t.

Pero se podía considerar otro tipo de proporción, por ejemplo que reducir continuamente a la mitad V₀ se corresponde a tomar continuamente raíces cuadradas de F/R₀. En términos modernos, diríamos que V debería ser proporcional al logaritmo de F/R.

La “Ley de Bradwardine” fue ampliamente aceptada hasta finales del siglo XVI, pero como la formulación inicial de Aristóteles, era errónea. Fue Newton quien formuló la ley que hoy conocemos como verdadera.

Bradwardine es autor también de otras interesantes obras matemáticas. Creó una teoría de polígonos estelares regulares en su libro Geometria speculativa, de 1496. Recordemos como se construyen polígonos estrellados. Si a partir de los vértices de un polígono regular de p lados se unen sus vértices alternadamente, es decir, cada q vértices (orden q) sucesivamente hasta alcanzar el vértice inicial, se obtiene un polígono regular estrellado, cuyos lados y ángulos son todos iguales. La figura que se obtiene puede representarse mediante la expresión {p/q}. Por ejemplo, a partir de un pentágono regular (p = 5) puede trazarse una estrella de cinco puntas uniendo el primer vértice con el tercero (q = 2), el tercero con el quinto, el quinto con el segundo, el segundo con el cuarto y el cuarto con el primero. Se obtiene así el polígono estrellado {5/2}. Para generar un polígono estrellado, la fracción p/q debe ser irreducible, esto es, p y q han de ser primos relativos.

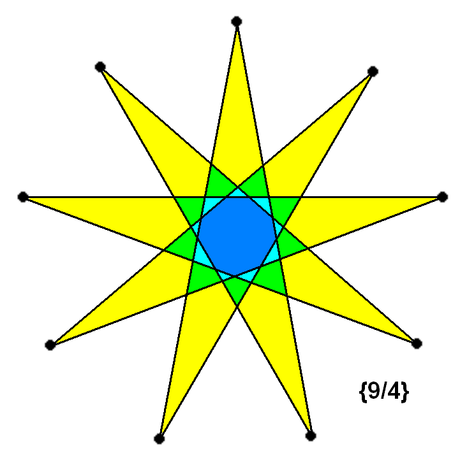
Los polígonos se pueden clasificar por orden y especie: dos polígonos son del mismo orden si tienen un número igual de lados mientras que dos polígonos son de la misma especie si la suma de sus ángulos es igual. Bradwardine probó resultados vcomo estos: el primer polígono estelar regular de la segunda especie es el polígono de cinco lados; la suma de los ángulos del polígono estelar de cinco lados es igual a los ángulos rectos; o el polígono es el primer polígono estelar regular de la tercera especie. Estableció además este principio general: el primer polígono estelar regular de cualquier especie se obtiene extendiendo los lados de la tercera figura constructible de la especie anterior.

En conjunto, la obra de Bradwardine es excepcional, y en cuanto a la ciencia su gran logro fue impulsar la idea de que las leyes naturales solo se pueden entender al expresarlas en una formulación matemática.

___________

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).