Los científicos se lo montan con modelos

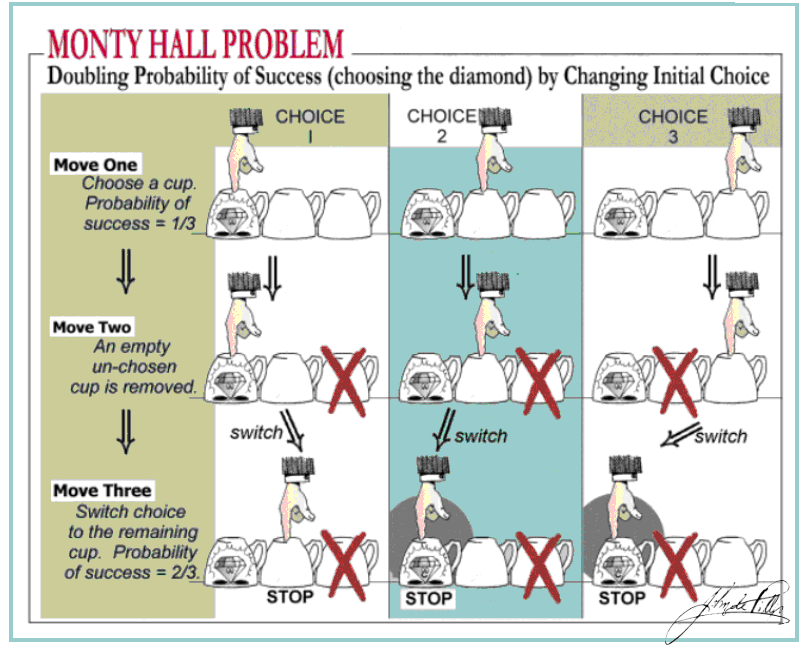
La importancia de tener un modelo para pensar sobre la realidad nunca debe ser desdeñada. De otra manera es difícil saber de qué estamos hablando. Véase, si no, esta entrada en el Otto Neurath o esta otra mía semanas atrás. Uno de los ejemplos más sencillos, a la vez que ilustrativo, es la paradoja de Monty Hall.
Monty Hall es el presentador de un concurso televisivo. Una de las situaciones en las que se suelen ver inmerso el concursante es la siguiente. Debe elegir entre tres puertas, una de las cuales tiene tras ella un premio. Las otras dos no guardan nada. El concursante elige la puerta A y, a continuación Monty Hall abre una de las otras dos puertas, pongamos que sea la B, y se ve que no hay premio. Monty Hall le da la oportunidad al concursante de cambiar y elegir la C, si quiere. ¿Debe el concursante cambiar de puerta?
Esta es una vieja paradoja y no es mi intención elaborar sobre ella. Sólo la tomo de referencia para ilustrar la necesidad de los modelos. Tal como yo he descrito la historia, nos falta saber cómo se ha llegado a la situación descrita. En particular, es necesario saber si Monty Hall sabía dónde estaba el premio y si, sabiéndolo, deliberadamente escoge la puerta en que sabe que no está.
Si Monty Hall abre una puerta al azar y sucede que no hay premio, las probabilidades a priori de que el premio esté tras A o tras C siguen siendo iguales (el 1/3 de probabilidad de B se pasa a medias a A y a C, quedando en 1/2 cada una) y el concursante no gana nada por cambiar.
Si, en cambio, Monty Hall sabe dónde está el premio y abre una puerta donde sabe que no está, la probabilidad de 1/3 de B se va toda a C, de manera que al concursante le conviene cambiar.
El modelo lo es todo. Intentar responder a la cuestión sin especificar qué caso tenemos en mente solo nos puede llevar a un gran dolor de cabeza tras una larga discusión.
Aclaro dos cosas. La formulación original de la paradoja narraba el segundo escenario. Sin embargo, mucha gente pensaba que la solución seguía siendo 1/2 y que no hacía falta cambiar. No me molesto en hacer los cálculos y las explicaciones de cómo se llegan a estas conclusiones porque está en cualquier página dedicada al asunto, incluidas las entradas en la wikipedia y en la ilustración que abre esta entrada. Pinchad sobre ella para verla completa.