Los tiburones de Vito Volterra

Umberto D´Ancona (1896 –1964) fue un biólogo italiano, nacido en Fiume el 9 de mayo de 1896. Comenzó sus estudio de Biología en Budapest, pero fueron interrumpidos por el estallido de la Primera Guerra Mundial. D´Ancona destacó por su valor militar y fue condecorado, retomando sus estudios en la Universidad de Roma.

Vito Volterra y Umberto D´Ancona

A mediados de los años 1920 D’Ancona estudiaba las poblaciones de peces en el mar Adriático, tomando datos en los puertos de mar que él bien conocía: en Fiume, Trieste y Venecia. Observó que durante la guerra, el porcentaje de tiburones y depredadores similares había aumentado, lo que entendía, ya que al reducirse la pesca de sardinas, jureles, etc. por parte de los pescadores, estos aumentaban y por lo tanto los peces grandes también lo hacían. Pero la pregunta que se hacía era: ¿cómo afectaba esta reducción de la pesca a los peces pequeños? El porcentaje no aumentaba, sino que disminuía.

Por aquel entonces, D´Ancona cortejaba a Luisa Volterra, con la que contrajo matrimonio en 1926, y que era hija del famoso matemático Vito Volterra (1860 – 1940). D´Ancona consultó el problema a su futuro suegro, y esta consulta condujo a desarrollar el llamadao modelo de predador-presa de Lotka-Volterra.

Alfred J. Lotka

El coautor de ese modelo es el matemático y químico norteamericano Alfred James Lotka, quién trabajó de manera independiente a Volterra y simultáneamente llegó a los mismos resultados.

Podemos buscar los antecedentes en los trabajos del clérigo británico Thomas Robert Malthus (1766-1834), quién en su libro de 1798, Ensayo sobre el principio de la población (An Essay on the Principle of Population), reeditado y ampliado en 1803, plantea el problema del crecimiento geométrico de la población contra el aritmético de los recursos alimenticios.

Pierre Francois Verhulst

Después de haber leído el “Ensayo sobre el principio de población” de Thomas Malthus, el matemático belga Pierre François Verhulst (1804-1849) en 1838, obtiene la ecuación logística para describir el crecimiento auto-limitado de una población biológica. Es precisamente Alfred J. Lotka quien deduce de nuevo la ecuación en 1925, llamándola “ley del crecimiento poblacional”. Esta es la ecuación logística:

donde P representa el tamaño de la población, t el tiempo, r es la tasa de crecimiento y K la capacidad de persistencia.

Las ecuaciones de Lotka-Volterra describen la evolución de un sistema en el que coexisten una especie de predadores y una de presas, y se escriben así:

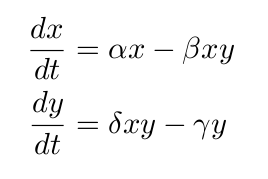
donde x es el número de presas, y es el número de predadores, dy/dt y dx/dt representa la tasa de crecimiento de cada una de las poblaciones, t es el tiempo, y α, β, γ, δ son parámetros.

Tanto la ecuación logística como las ecuaciones de Lotka-Volterra, se usan en muchos ámbitos, no sólo para estudiar problemas de dinámica de poblaciones. Sobre estos temas volveremos en Matemáticas y sus fronteras, aprovechando la ocasión que ofrece el Año Internacional de la Biología Matemática.

_______

Manuel de León (CSIC, Fundador y Director del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU).