Matemáticas y cabellos

“Observa el movimiento de la superficie del agua que se asemeja a la del cabello, y tiene dos movimientos, uno de los cuales continúa con el flujo de la superficie, el otro forma las líneas de remolinos.”

Leonardo de Vinci: “Sobre las proporciones y sobre los movimientos de la figura humana”.

Hace unas semanas, de una manera muy casual, encontré en mi muro de Facebook una anécdota que contaba Peter Lax. Una vez, cuando Lev Landau estaba visitando el Instituto de Estudios Avanzados (IAS) de Princeton, Einstein se disculpó con Landau, porque tras su paseo con su correspondiente charla,  los periodistas los habían en busca de un pronunciamiento de Einstein sobre algún evento mundial. “Lev, no puedo evitarlo, ya sabes cómo son”, se disculpó Einstein, y Landau respondió: “Albert, ¿alguna vez has considerado cambiar tu peinado?”. Claro que Landau no andaba tampoco libre de pecado. Esto me llevó a pensar sobre que piensan los matemáticos y los físicos de sus cabellos, y resulta que el tema es más profundo de lo que uno podría pensar en un principio.

Albert Einstein

Lo que mucha gente ignora es que las grandes compañías que se dedican a la fabricación de champús, acondicionadores, tintes, y todo tipo de productos relacionados con el cabello están interesadas en la investigación del pelo que cubre nueatras cabezas, y que tiene que ver no sólo con la química, sino, y mucho, con las matemáticas y la física.

Lev Landau

Uno de los primeros interesados en analizar la naturaleza de los cabellos fue Hooke, que en su obra Micrographia (1665) presentaba dibujos de cabellos gracias al uso del microscopio. Hooke vio como los pelos son cilindrícos, cona capa extreior llamada cutícula y una microestructura interna constituida por ima proteína, la queratina. Tenemos entre 50.000 y 100.000 pelos en nuestra cabeza que crecen como 1cm cada mes. Un cabello es elástico, así que podemos aplicar a su estudio lo que conocemos de la mecánica de continuos.

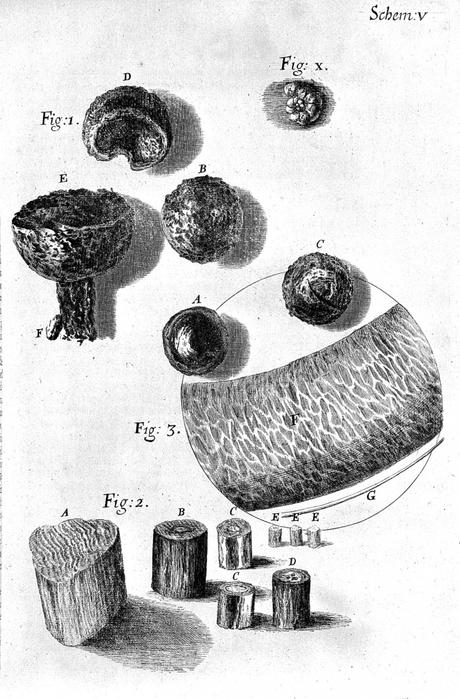
Varios tipos de cabello en la obra Micrographia de Robert Hooke

Aunque un cabello es algo muy pequeño, si podemos medir como la gravedad le afecta, lo que hará en más meduda en relación con la longitud (no olvidemos que un cabello tiene una masa).

Otro aspecto que es importante es la que podíamos llamar la curvatura intrínseca del cabello, su ondulación, que variará de un individuo a otro.

Usando ahora el cálculo de la energía por unidad de longitud para filamentos elásticos obtenida por Leonhard Euler y Jakob Bernoulli, R.E. Goldstein, P.B. Warren y R.C. Ball fueron capaces de obtener una fórmula para la energía de un haz de cabellos (en su artículo Shape of a Ponytail and the Statistical Physics of Hair Fiber Bundles, Phys. Rev. Lett. 108, 078101 (2012)). Analizaron así diferentes formas de colas de caballo, que, asombrosamente, muetsran como la presión es una función lineal actuando como una simple ley de Hooke.

Si están más interesados en este tema, pueden leer con atención la presentación Leonardo, Rapunzel, and the Mathematics of Hair, del propio  Raymond E. Goldstei,  donde además analiza el movimiento de una cola de caballo. Por ejemplo, si una corredora lleva un peinado de cola de caballo, aunque su cabeza sube y baja, la cola se mueve de un lado a otro. La explicación hay que buscarla en los resultados del matemático George William Hill en mecánica celeste (lo que ocurre cuando un parémtro se hace oscilar peridicamente).

Decir finalmente que esta investigación sobre las colas de caballo es una primera aproximación para entender como el cabello se enreda, cosa que más de una vez hemos experimentado al peinarnos.

Si usted cree que hemos acabado con las matemáticas y el cabello, vea este artículo Mathematical Patterns in African American Hairstyles, de Gloria Gilmer de. En él se analizan los diseños y los patrones en los peinados de mujeres (y hombres) de origen afroamericano. La autora se hace la siguiente pregunta: “¿Qué puede contribuir los distintos trenzados de pelo a la educación matemática y, a la inversa, qué puede contribuir la educación matemática a la la innovación del trenzado de pelo?” Hay muchas matemáticas en esos peinados y les invito a leer el artículo para descubrirlas.

Y podríamos hablar también del uso de las matemáticas para colorear el cabello de un cliente. El estilista combina los colores primarios para resaltar o disminuir ciertos tonos para que el cliente obtenga lo que desea, y esto es un asunto de proporciones. Y también la geometría se usa en la elaboración de los cortes de cabello.

Les dejo con este video

¡Y piensen en las matemáticas la próxima vez que vayan a la peluquería!

__________

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias)