 La comunidad
biológica
La dinámica de las
poblaciones
Introducción a las
dinámicas de las poblaciones en unacomunidad
Modelo Lotka-Volterra
depredador-presa
Sucesiones de una
comunidad biológica
La comunidad como un
sistema complejo y multivariable
Estudio continuo de
las dinámicas de las poblaciones en una comunidad
La comunidad
biológica
La dinámica de las
poblaciones
Introducción a las
dinámicas de las poblaciones en unacomunidad
Modelo Lotka-Volterra
depredador-presa
Sucesiones de una
comunidad biológica
La comunidad como un
sistema complejo y multivariable
Estudio continuo de
las dinámicas de las poblaciones en una comunidad
Modelo Lotka-Volterra depredador-presa Introducción
Aunque mucho podría indagarse sobre la matematización de la ecología por parte de matemáticos como Volterra o Kolmogorov, por el momento nos enfocaremos exclusivamente a una serie de conclusiones muy sencillas.
Este dialogo empieza por las funciones que nos sirven para describir la densidad poblacional, es decir, el modelo exponencial y el modelo logístico exponencial.
Recordando la matemática de poblaciones, tenemos que el modelo logístico exponencial es el que mejor se adecua a los problemas de los sistemas reales, en especial los recursos limitados que proviocan que las poblaciones no puedan crecer a un nivel infinito.
Ecuación logística exponencial
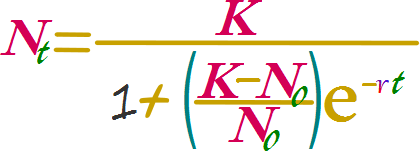
Forma "integrada" del modelo logístico exponencial.
Tasa de cambio de la ecuación logística exponencial
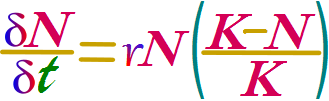
Forma "derivada" del modelo logístico exponencial, que describe solo las tasas de cambio.
Gráfica de la función logística exponencial
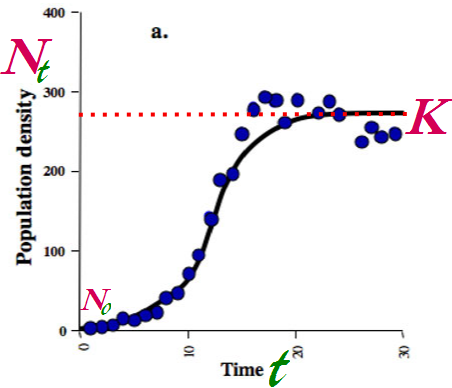
Figura LV-01. Gráfica de la forma integrada del modelo logístico exponencial, es una gráfica bastante típica con forma sigmoide "s", la cual se puede describir en cuatro fases, la primer fase es la de crecimiento logarítmico y es muy lenta, representa el momento en que una población pequeña se adecua a su ambiente; posteriormente la fase exponencial que se caracteriza por rápido crecimiento, luego está la fase de frenado en que la población empieza a reproducirse con mas lentitud. Finalmente la población alcanza el límite o capacidad de carga de un sistema.
Ahora bien, las ecuaciones Lotka-Volterra nos permite graficar el cambio de las poblaciones de dos especies A y B a lo largo del tiempo, donde ambas gráficas se encuentran vinculadas entre sí mediante una interacción ecológica, como la depredación.
Así, al adicionar un modificador a la ecuación logística y vincular dos de estas ecuaciones para cada una de las especies se obtiene el modelo que generalmente es reconocido en la literatura como el modelo Lotka-Volterra de depredadores y presas.
Si se tienen dos especies a las cuales llamaremos X y Y, se tiene que una especie causa un efecto negativo en la otra, mientras que la relación inversoa es positiva. Adicionalmente, ambas especies crecen de una manera logística exponencial. Al igual que sucede con la logística, las ecuaciones L-V se expresan generalmente en términos de su tasa de cambio “derivada” no no en términos de sus valores absolutos “integrada”
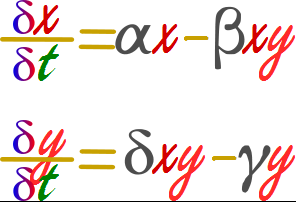
Alfa: Coeficiente de repruduccion de las presas, es decir su valor de (r). Beta: Coeficiente que define la probabilidad de que una presa sea comida por un depredador Gamma: Coeficiente de Decaimiento de los depredadores. Si no hay presas que comer, el depredador se muere. Delta: Coeficiente que define la probabilidad reproducción del depredador tras comerse a una presa, es decir su valor de (r).
Al integrar y resolver ambas funciones “formas integradas del modelo de Lotka-Volterra que es verdaderamente difícil de encontrar en los textos de introducción a la ecología matematizada” se nos genera una gráfica muy particular.
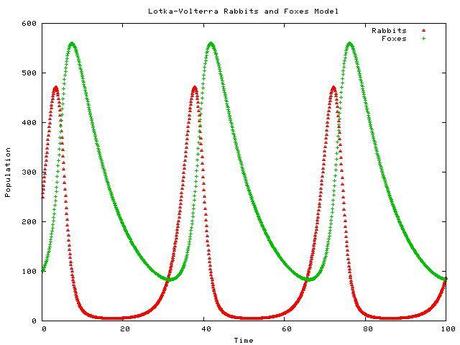
Figura LV-02. La gráfica del modelo LV es típico, asemejándose a una gráfica simultánea del senx y cosx, en este caso la población de presas al llegar a un punto interior a la capacidad de carga es abrumada por la población de depredadores, pero cuando las presas se hacen menos comunes, los depredadores también sufren.
Se puede observar que el cambio en la población de presas es acompañado por un cambio en la población de depredadores similar, pero desfasado en el tiempo, operando dentro de un rango de valores, es decir, dentro de un equilibrio dinámico. Lo que le sucede a las presas afecta a los depredadores a largo plazo, y un desequilibrio en la población de cualquiera de los dos afecta a su compañero.
Por otro lado, la gráfica de la relación L-V no solo arroja un equilibrio dinámico, en ocasiones se pueden presentar equilibrios inestables, o equilibrios estabilizantes.
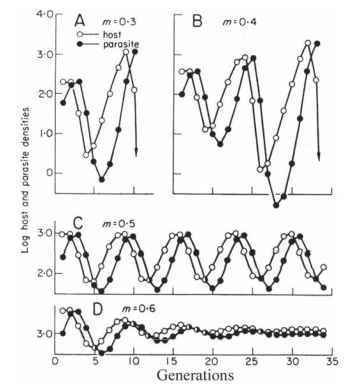
Figura LV-03. Las oscilaciones en el modelo LV son diferentes dependiendo del sistema, en A y B tenemos equilibrios muy inestables, de hecho en B la población de parásitos se extinguió en ese sistema, por lo que una nueva población inicial debió haber reingresado desde sistemas adyacentes. en C tenemos un equilibrio estable aunque sus oscilaciones son peligrosamente altas en términos del número de individuos, mientras que en D tenemos un equilibrio que tiende a la estabilización de ambas poblaciones. Resulta notable que el modelo de depredador presa también pueda aplicarse a la relación de simbiosis parasítica. es probable que D represente la evolución de un parasitoide que mata a su hospedero a un parásito que no necesariamentelo mata, hasta un comensal que no afecta la población del hospedero.
Sin embargo este fenómeno no se observa de manera tan clara en la naturaleza debido a que los depredadores tienen más de una presa a la cual cazar. Cuando una presa se hace muy común es fácil cazarla, pero cuando su población desciende, es más fácil cazar otras especies, esto le da la oportunidad a la primer población de presas de recuperar sus números de individuos sin que su población tenga que disminuir de una manera tan drástica.
Con tan solo adicionar una tercera especie, otra presa tenemos un efecto de amortiguamiento de la depredación en la población de presas “en ingles se usa con frecuencia el nombre de buffer al efecto de amortiguamiento”.
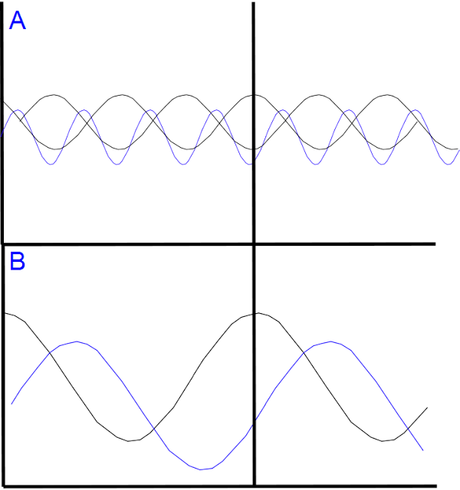
Figura LV-04. Tenemos en B una relación entre un depredador y una presa, sus oscilaciones son mas amplias ya que con una sola presa, esta enfrenta mas presión del depredador, por lo que tarda mas tiempo en regenerar su población. Lo mismo para el depredador, mientras mas difícil es encontrar la presa, sus números se mantienen ambos por mas tiempo. en A tenemos un modelo con dos presas, que permite el mantenimiento de un equilibrio menos inestable, ya que el depredador puede alternar entre una presa y otra a medida que una población decrece y otra aumenta.
Lo anterior implica que, los números para la cantidad de individuos de cada especie variaran en una comunidad como función del número de especies, así entre mayor es el número de especies en una comunidad, menor es la oscilación de las poblaciones, lo que hace que la comunidad sea más estable y tenga menores riesgos de generar una extinción espontánea.
Las comunidades ecológicas con menor número de especies tienden a tener una mayor variación en su número de individuos, lo cual puede provocar riesgos de extinciones locales o globales de una especie o grupos de especies interrelacionadas. PRINCIPAL
REGRESAR
