MOSS para un problema Bandido Multibrazo (Multi-Armed Bandit)

MOSS (Minimax Optimal Strategy in the Stochastic case, Estrategia Óptima de Minimax en el caso estocástico) es una variante de UCB1 que se presenta como una aproximación generalizada, de modo que puede ser utilizado con cualquier tipo de bandido.

MOSS

En la estrategia MOSS modifica la expresión que calcula en intervalo de confianza. Para ello se sustituye el término en el logaritmo de del número de veces que se ha jugado con todos los bandidos,

por el cociente del número de veces que se ha jugado con todos los bandidos entre el producto de número de bandidos por las veces que se ha jugado con el bandido bajo evaluación

log{\frac{N}{k n_j}}.

Valor que puede ser negativo y, para evitar problemas a la hora de sacar la raíz cuadrada, es necesario limitar el valor a 0. Esto es, el intervalo de confianza para el bandido j ahora es:

\varepsilon_j = \sqrt{\frac{\min \left(\log{\frac{N}{k n_j}},0\right)}{n}}

Ahora, para seleccionar en cada una de las jugadas un bandido el algoritmo MOSS buscará aquel cuya recompensa esperada más intervalo de confianza sea mayor. Esto es, se seleccionará el bandido en base a la siguiente expresión:

X_{MOSS{j}} = \bar{X_j} + \sqrt{\frac{\min \left(\log{\frac{N}{k n_j}},0\right)}{n}}

Implementación de MOSS en Python

Una vez definida la fórmula con la que se selecciona el bandido en cada una de las jugadas podemos proceder a la implementación de algoritmo en Python. Para ello, al igual que en la implementación de UCB1, nos basaremos en la clase Epsilon que se creó para Epsilon-Greedy con decaimiento. De este modo el código de MOSS se queda simplemente en

class MOSS(Epsilon):
    def __init__(self, bandits):
        self.bandits = bandits
        
        self.reset()
    
    def select(self):
        num_bandits = len(self.bandits)
        total = len(self._rewards)
        
        if total < num_bandits:
            bandit = total
        else:
            moss = [0] * num_bandits
            
            for i in range(num_bandits):
                moss[i] = self._mean[i] + np.sqrt(max(0, np.log(total/(num_bandits * self._plays[i]))) / self._plays[i])
        
            max_bandits = np.where(moss == np.max(moss))[0]
            bandit = np.random.choice(max_bandits)
            
        return bandit
    
    
    def reset(self, initial=None):
        self._rewards = []
        self._plays = [0] * len(self.bandits)
        self._mean = [0] * len(self.bandits)

En primer lugar, dado que es necesario haber jugado por lo menos una vez con cada uno de los bandidos para poder aplicar el algoritmo, las primeras jugadas serán deterministas seleccionado una vez cada uno de los bandidos. Posteriormente, en cada una de las jugadas se seleccionará el bandido que determine el algoritmo o, en caso de empate, uno de ellos al azar.

Resultados de MOSS

Para comprobar el rendimiento de MOSS se puede usar la clase Bandit basada en una distribución binomial implementada en valores iniciales optimistas. Comparando los resultados con los obtenidos para UCB1. De forma análoga a cómo se hizo en ocasiones anteriores, se puede usar el siguiente código.

np.random.seed(0)

bandits = [Bandit(0.02), Bandit(0.06), Bandit(0.10)]

moss = MOSS(bandits)
ucb1 = UCB1(bandits)

moss.run(200000)
ucb1.run(200000)

moss.plot(True, label='MOSS')
ucb1.plot(True, True, label='UCB1')
plt.legend()

Lo que produce la siguiente gráfica.

Evolución de la recompensa promedio con el numero de tiradas para el algoritmo MOSS y UCB1 con tres bandidos basados en una distribución binomial

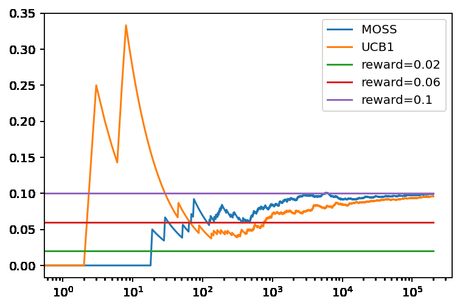
En la que se puede ver que, para el caso evaluado, MOSS converge más rápidamente al resultado óptimo debido a que juega menos veces con los bandidos que no son óptimos. Ya que solamente ha seleccionado 635 veces el primer bandido, mientras que UCB1 3070, y 1311 veces el segundo bandido, mientras que UCB1 10.135.

Conclusiones

En esta ocasión hemos visto MOSS, otra variante de UCB1, para resolver el problema del Bandido Multibrazo. Algoritmo que mejora el rendimiento frente a UCB1 ya que selecciona en menos ocasiones un valor que no es óptimo.

Con esta entrada cerramos el repaso de los algoritmos para la resolución del problema Bandido Multibrazo que hemos realizado en las últimas semanas.

Imagen de Muhammad Ikram Ul Haq en Pixabay