Movimiento rectilíneo Parte 2

Problema 1
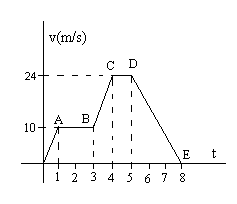
Un móvil describe un movimiento rectilíneo. En la figura, se representa su velocidad en función del tiempo. Sabiendo que en el instante t=0, parte del origen x=0.

• Dibuja una gráfica de la aceleración en función del tiempo
•  
• Calcula el desplazamiento total del móvil, hasta el instante t=8s.
•  
• Escribe la expresión de la posición x del móvil en función del tiempo t, en los tramos AB y BC

Interpretacion Grafica 
 Solucion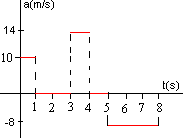

Aceleraciones: pendientes de las rectas (véase la gráfica)
Desplazamiento entre los instantes t=0 y t=8 s: área bajo la curva v-t.
Δx=5+20+17+24+36=102 m

Tramo AB

x=5+10(t-1)=10t-5 m

Tramo BC

x=25+10(t−3)+1214(t−3)2

Problema 2
Un automóvil parte del reposo y se mueve con aceleración constante de 4 m/s², y viaja durante 4 s. Durante los próximos 10 s se mueve con movimiento uniforme. Se aplican los frenos y el automóvil decelera arazón de 8 m/s² hasta que se detiene.

• Calcular el desplazamiento del móvil en cada intervalo y el desplazamiento total.
•  
• Hacer un gráfico de la velocidad en función del tiempo.
•  
• Mostrar que el área comprendida entre la curva y el eje del tiempo mide el desplazamiento totla del automóvil

Solucion
De t=0 a t=4.
a=4  v=4t  x=124t2
Para t=4 s, v=16 m/s, x=32 m
De 4 s a 14 s
 a=0  v=16  x=32+16(t−4)
Para t=14 s, v=16 m/s, x=192 m
De 14s hasta que se para
a=−8  v=16+(−8)(t−14)  x=192+16(t−14)+12(−8)(t−14)2
Se detiene v=0, en el instante t=16 s, la posición del móvil es x=208 m
Gráfica

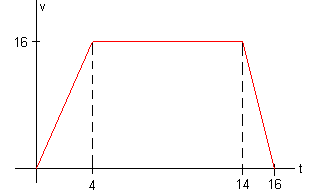
Área bajo la curva v-t
4⋅162+10⋅16+2⋅162=208
Con estos dos Ejemplos vamos Abarcando el Tema de Movimiento rectilíneo.