Movimiento rectilíneo Parte 4

Interpretación geométrica de la derivada

El siguiente proceso, nos puede ayudar a entender el concepto de derivada y la interpretación geométrica de la derivada

v=limΔ t→0ΔxΔt=dxdt
Se elige la función a representar,  entre las siguientes:
x=16t3−73t2+172tx=13t+5x=8⋅sin(π10t)
Ejemplo:
Elegimos la primera función y el punto t₀=3.009
Elegimos ampliación 1000.  La pendiente de la recta vale -1, y se muestra en la figura.

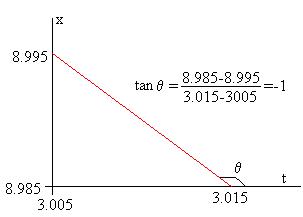
La derivada de dicha función es
dxdt=12t2−143t+172