Hace unos años tuve la oportunidad de leer "El Enigma de Fermat", de Simon Singh. Un maravilloso libro en el cual se explicaba la historia de una aparente sencilla conjetura, que según Pierre de Fermat era fácilmente demostrable según una genial demostración que las reducidas dimensiones del margen de la hoja de un libro no le permitía reproducir. Pena, de margen!! porque el encontrar esta demostración tuvo ocupados a los mejores matemáticos durante 350 años, hasta que Andrew Wiles pudo demostrar que la conjetura era falsa. Este honor y esta recompensa a su esfuerzo permitió a Andrew Wiles conseguir una recompensa económica sustanciaosa que se había ofrecido para intentar animar a demostrar uno de los considerados problemas más difíciles de la historia.
Las recompensas económicas, empiezan a ser algo bastante habitual e incluso normal y justas diría yo, dado que implicarse en resolver un enigma de este tipo supone dedicar gran parte de la vida de estos Indiana Jones de las matemáticas, e intentar algo que muchas veces no conduce al éxito, como podemos leer en la también excelente novela de "El tío Petros y la conjetura de Goldbach".
En el año 2000, el Clay Mathematics Institute creó siete premios de un millón de dólares, que son ahora conocidos como los Problemas del Milenio. Uno de ellos, la Conjetura de Poincaré, fue resuelta en 2002 por el matemático ruso Grigori Perelman, quien rechazó la gratificación económica.
Ahora, una nueva recompensa aparece por resolver una conjetura como se cuenta hoy en el periódico ElPais. En este caso para resolver la conjetura de Beal:
La ecuación establece que si Ax+ By= Cz A, B, C, x, y, z enteros positivos, siendo x, y, z mayores que 2, entonces A, B, C deben tener un factor común primo. La conjetura implica el teorema de Fermat del que hablábamos.
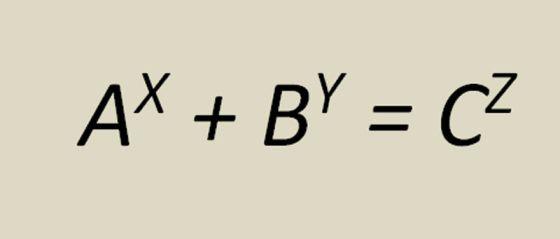Si quieres saber más sobre la conjetura de Beal, clica aquí para ir al artículo de ElPais VER
Puzzle Bobble
Karate Blazers
Puzzle De Bloques
Magical Cat Adventure