Porcentajes

¿Es o no importante saber de porcentajes?
Quienes sigan el blog desde hace ya un tiempo sabrán que dimos respuesta a esta pregunta con un sencillo ejemplo en una entrada a la que llamé…
¿Por qué hay que saber de porcentajes?
… y la respuesta es SÍ, más que todo para que no nos engañen con facilidad.
Así es que tenemos que saber calcular porcentajes y también interpretarlos. Y eso es lo que pretende esta entrada.
Si consideras que ya dominas suficientemente el cálculo de porcentajes…
¡No te marches aún!
Esta entrada termina con una animación de 2 minutos titulada
“SI 100 PERSONAS VIVIERAN EN LA TIERRA”
que creo que te gustará bastante y es una auténtica interpretación de porcentajes.

Imagen capturada de la animación.
Empecemos…
¿Qué es un porcentaje?
Digamos que el porcentaje es una forma de comparar cantidades en la que se relaciona una parte con el total. Está asociado a una razón o proporción.
Se le llama comúnmente tanto por ciento, donde “por ciento” significaría “de cada cien unidades“. El tanto por ciento de una cantidad, donde “tanto” sería un número, se refiere a la parte proporcional a ese número de unidades de cada cien de la cantidad total.
Bueno, aunque dé la sensación de ser un lío, es mucho más sencillo de lo que parece, y es que a veces definir algo es más complicado que lo que se está definiendo.
Vamos con el cálculo, que probablemente sea lo que más os interese de todo esto.
Para ello, analizaremos las distintas situaciones que se nos pueden presentar (lo que serían los tipos de problemas) con ejemplos concretos, que es como mejor se ve.
¡Os aviso!
No me gusta eso de aprenderse una fórmula para cada caso y hacer después las cosas de forma mecánica sin saber de dónde viene y por qué. Creedme si os digo que eso no os llevará muy lejos.
Así que, ya que hemos dicho que el porcentaje está asociado a una razón o proporción, vamos a ir directamente a la “raíz” de todo esto y partiremos siempre de una regla de tres simple directa.
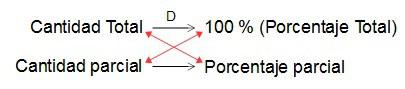
De aquí, según sea el caso, necesitaremos calcular: la cantidad total, la cantidad parcial, o el porcentaje parcial. Lo demás serán números que conocemos.
Primera situación:
Dada una cantidad total, por ejemplo 90 personas, queremos saber cuánto es un porcentaje parcial, por ejemplo el 20 %:
Nos “hacemos” nuestra regla de tres con los valores que conocemos…
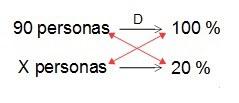
Es el único valor en la regla de tres que hemos planteado que no conocemos, pues los demás son valores conocidos.
Así que aplicamos la regla de tres simple directa para calcularlo (si tenéis alguna duda en cómo se aplica una regla de tres simple directa lo tenéis explicado con detalle en esta entrada: Regla de tres)…
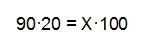
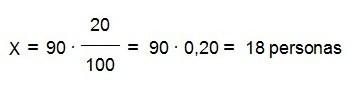
El 20 % de 90 personas son 18 personas.
Si os fijáis, lo que hemos hecho es multiplicar la cantidad total por 20 y dividir entre 100 ó, lo que es equivalente, multiplicar por 0,20.
Si, por ejemplo, hubiésemos querido calcular el 60 %, multiplicaríamos la cantidad total por 0,60; Si el porcentaje a calcular fuese un 5 %, multiplicaríamos en ese caso por 0,05 (resultado de dividir 5 entre 100).
Por cierto, siempre que estemos calculando una parte del total nos debe salir una cantidad menor que la total. Si no es así es obvio que algo estamos haciendo mal, porque no tendría sentido.
Otra situación posible:
Calcular el total, dada una cantidad que corresponde a un porcentaje de él.
Ejemplo: En una clase hay 4 alumnos de pelo rubio y son el 16 % del total de la clase ¿cuántos alumnos hay en total?
Montamos de nuevo nuestra regla de tres, en la que ahora el único valor que no conocemos es obviamente el que queremos calcular: la cantidad total de alumnos (los alumnos que hay en la clase)…
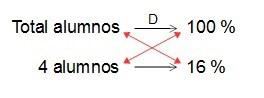
Y calculamos…

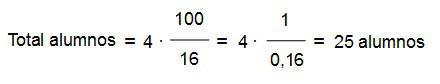
En una clase en la que 4 alumnos son el 16 % del total, la cantidad total de alumnos es de 25.
¿Qué es lo que hemos hecho en esta segunda situación?
Es justo la inversa de la anterior.
Es decir, en la primera queríamos obtener, partiendo de la cantidad total conocida, la cantidad parcial que correspondía a un porcentaje parcial; Y en esta segunda situación lo que queremos averiguar es, partiendo de la cantidad parcial conocida correspondiente a un porcentaje parcial, la cantidad total.
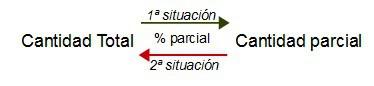
Por eso, si observamos las operaciones que hemos hecho en el cálculo, antes (en la primera situación) habíamos multiplicado la cantidad total por 0,20 (el porcentaje parcial era del 20 %) y ahora (en esta segunda situación) hemos dividido la cantidad parcial por 0,16 (el porcentaje parcial es en este caso del 16 %), justo la operación inversa (la división es la operación inversa de la multiplicación).
A este factor por el que multiplicamos la cantidad total o dividimos la cantidad parcial, según sea el caso, podríamos llamarle factor de porcentaje.

Este último método, el de multiplicar o dividir por ese factor de porcentaje es el que se suele emplear para ganar mayor rapidez en los cálculos y cuando ya se controla correctamente el cálculo de porcentajes (cuando estamos seguros de que lo vamos a aplicar de forma correcta).
No obstante, como ya indiqué y hemos podido comprobar, tiene su origen en la regla de tres simple directa que habíamos visto, la recuerdo…
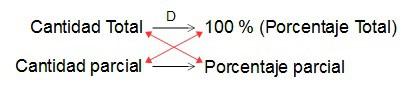
y siempre podemos recurrir a ella para evitar confusiones y errores.
¡Espera que aún no hemos terminado!
Vamos a ver una tercera situación que, además, probablemente sea la que en mayor número de ocasiones nos encontremos…
Dado el total y una parte de él, calcular que % es esa parte del total.
Ejemplo: En una estantería hay 60 discos de música, de los cuales 15 son de Heavy ¿qué porcentaje de discos de Heavy hay en la estantería?
Vamos allá… regla de tres…
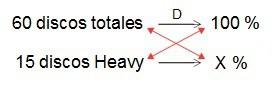
Aquí lo que no conocemos es el porcentaje parcial (le hemos llamado X %).
Aplicamos la regla de tres simple directa:
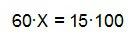
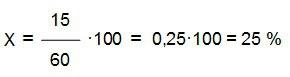
Hay un 25 % de discos de Heavy en la estantería (por cierto que en la mía es muchísimo más alto).
Como podéis observar, calcular el porcentaje (%) que supone una parte respecto del total es bastante sencillo, y tan solo hay que dividir la parte entre el total (obtendríamos así el factor de porcentaje del que hablábamos) y multiplicar por 100 para expresarlo en tanto por ciento.
Pero vuelvo a repetir que siempre podemos echar mano de la regla de tres, que es muy socorrida en estos casos.
¿Tenéis ganas de ver el vídeo ya, verdad?
Lo sé pero, a riesgo de resultar pesado, esta entrada no sería completa si no hablase de los aumentos y disminuciones porcentuales. Así que, con vuestro permiso vamos a verlos, que más de uno o una me lo agradecerá porque es precisamente donde más se suelen cometer errores.

Aumentos porcentuales.
Pueden darse distintas situaciones…
Incrementar una cantidad en un porcentaje.
Ejemplo: En un folleto de unos grandes almacenes hemos visto un televisor que nos ha gustado por 230 euros. Sin embargo junto al precio aparece un pequeño asterisco que nos lleva a una nota al pie de la página que dice que ese precio es “IVA no incluído”. Sabiendo que el IVA (Impuesto sobre el Valor Añadido) en España es del 21 % ¿Cuánto cuesta el televisor?
Con lo que hemos visto ya antes, resolver este tipo de situaciones es bastante sencillo: primero calculamos lo que representa el porcentaje de esa cantidad y después se lo sumamos (porque es un incremento) a dicha cantidad.
Vamos a hacerlo así aunque, como en los casos anteriores, veremos después una forma mucho más rápida de calcularlo.
En nuestro ejemplo, primero calculamos el 21 % de 230 euros (podemos hacerlo partiendo de una regla de tres o directamente multiplicando por el factor de porcentaje, que aquí sería 0,21)…
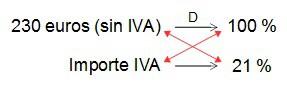

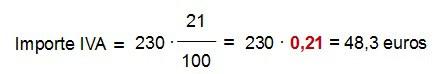
Y ahora se lo sumamos al precio inicial…

El televisor cuesta, incluyendo ya el IVA, 278,3 euros.
¡Vaya, ya no parece tan barato!
He prometido antes una vía más rápida de cálculo, así que vamos a verla. Escribamos lo que hemos hecho utilizando el factor de porcentaje…
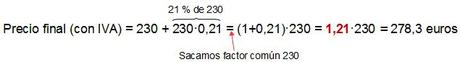
Es decir, para incrementar la cantidad inicial en un 21 % bastaría con multiplicarla por 1,21.
Pero ¿qué es lo que estamos haciendo al multiplicar el valor inicial por 1,21?
Multiplicar el valor inicial por 1,21 no es otra cosa que calcular el 121 % del valor inicial (100 % + 21 % = 121 %)
Así, por ejemplo, si el incremento fuese de un 6 % multiplicaríamos la cantidad inicial por 1,06 (calcular el 106 %); Si fuese de un 70 % multiplicaríamos por 1,70 (calcular el 170 %); O, si fuese de un 250 %, multiplicaríamos la cantidad inicial por 3,50 (calcular el 350 %).
Es decir, este problema se puede plantear también directamente como el cálculo del 121 % del valor inicial, multiplicando el valor inicial por el factor de porcentaje del incremento 1,21, o planteando sólo una regla de tres:

y resolviendo obtendríamos el mismo resultado…

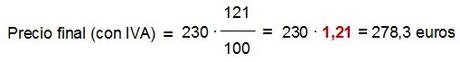
Cualquiera de las formas que hemos visto sería válida, pues en el fondo estamos haciendo lo mismo con más o menos pasos.
¿Y si lo que queremos es justo lo contrario?
Conocido el valor final y el porcentaje que se ha incrementado, queremos saber el valor inicial.
Ejemplo: En el año 2015 el censo de una ciudad ha registrado una población de 26.460 habitantes. Si ha habido un aumento del 5 % respecto del año anterior ¿Qué población tenía dicha ciudad en 2014?
¿Se os ocurre cómo hacerlo?
Podemos, por ejemplo, plantear una regla de tres como la última que hemos visto, pero siendo ahora el valor conocido el valor final (el número de habitantes en 2015) y el desconocido el valor inicial (el número de habitantes en 2014):

y aplicando la regla de tres simple directa…
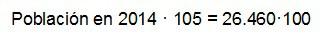
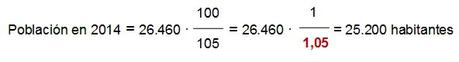
En 2014 la ciudad tenía una población de 25.200 habitantes..
Si os fijáis en esto último, así como para obtener en el caso anterior el valor final a partir del valor inicial multiplicábamos por el factor de porcentaje del incremento, para obtener el valor inicial conociendo el valor final y el porcentaje que ha aumentado, basta con dividir el valor final entre el correspondiente factor de porcentaje del incremento.
Si, por ejemplo, el incremento hubiese sido de un 12 % dividiríamos el valor final entre 1,12 (factor de porcentaje correspondiente al 112 %) para obtener el valor inicial.

Veamos ahora otra posible situación de aumento porcentual…
Una cantidad (un precio por ejemplo) ha aumentado de un valor inicial a un valor final y queremos saber en qué porcentaje se ha incrementado.
Ejemplo: El verano pasado la entrada a la piscina del pueblo donde vas a pasar las vacaciones costaba 1,5 euros. Este verano, el primer día de tus vacaciones allí, has ido a pagar para entrar y resulta que ahora cuesta 1,8 euros. Tú, presa de tu enfado y para poder quejarte con más argumentos, quieres calcular el porcentaje en que se ha incrementado el precio del verano pasado a éste.
Lo primero es calcular la diferencia entre el valor final y el valor inicial para saber en qué cantidad ha aumentado…

Y ahora vemos qué porcentaje representan esos 0,3 euros respecto del valor inicial.
Planteamos la correspondiente regla de tres (si lo tenemos muy claro podríamos ahorrarnos el paso de la regla de tres y, como ya vimos en su momento, dividir directamente la parte entre el total y multiplicar después por cien):
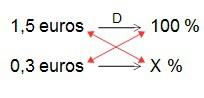
de donde…
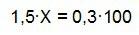
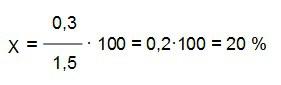
El precio de la piscina del pueblo ha aumentado del verano anterior a éste en un 20 %.
Y éste es el momento en el que nos quejamos y decimos con argumentos suficientes: ¡Qué barbaridad! ¡Son unos ladrones! ¡Un veinte por ciento!
Bien, nos quedan las disminuciones porcentuales que, salvo porque las cosas en lugar de aumentar disminuyen, funcionan análogamente a los incrementos porcentuales que acabamos de ver.
No obstante, vamos a verlo paso a paso como los anteriores.
Disminuir una cantidad en un porcentaje.
Por ejemplo: Llevas tiempo detrás de un videojuego, pero actualmente cuesta 45 euros y es demasiado para lo que puedes gastarte. En la tienda a la que sueles ir han anunciado que dentro de dos semanas lo van a rebajar un 30 % y quieres saber si esta vez te llegará el dinero que tienes para comprarlo. ¿Cuál será su precio cuando lo rebajen?
Si recuerdas, una forma de hacerlo es:
Calcular primero lo que representa el porcentaje de esa cantidad (el 30% de 45 euros) y después restárselo (porque es una disminución) a dicha cantidad (a 45 euros).
Para calcular el 30 % de 45 euros podemos recurrir a la regla de tres simple directa correspondiente o, como vimos, multiplicar directamente por el factor de porcentaje 0,30 (yo voy a poner la regla de tres para que se sepa cómo quedaría, que para correr y saltarse cosas ya están las clases habitualmente):
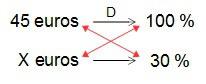
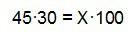
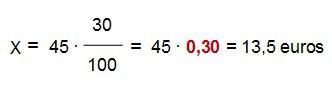
Y ahora se lo restamos al precio inicial…

Pues ya sabemos que el videojuego va a costar 31,5 euros dentro de dos semanas. Ya es cuestión de echar cuentas y valorar si nos va a interesar comprarlo o no.
Ahora, igual que hicimos con los aumentos porcentuales, vamos a deducir cómo se obtendría en este caso el factor de porcentaje de la disminución para poder calcularlo de forma más rápida y en un solo paso.
Para ello escribimos lo que hemos hecho utilizando el factor de porcentaje parcial del 30 %…
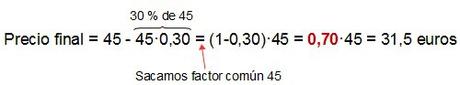
Es decir, para disminuir la cantidad inicial en un 30 % bastaría con multiplicarla por 0,70, que sería el factor de porcentaje correspondiente a la disminución al 70 %, pues lo que hemos hecho al multiplicar el valor inicial por 0,70 no es otra cosa que calcular su 70 % (100 % – 30 %).
Si, por ejemplo, la disminución fuese de un 8 % multiplicaríamos la cantidad inicial por 0,92 (calcular el 92%, resultado de restar al 100 % el 8 %); Si fuese de un 60 % multiplicaríamos por 0,40 (calcular el 40%, resultado de 100% – 60 %); O, si fuese de un 75 %, multiplicaríamos la cantidad inicial por 0,25 (calcular el 25%, resultado de restar al 100% el 75%).
Es decir, que como ocurría con los aumentos porcentuales, este problema se puede plantear diréctamente como el cálculo del 70 % del valor inicial, multiplicando por el factor de porcentaje correspondiente de 0,70, o planteando sólo una regla de tres:
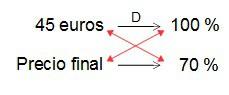
De donde…

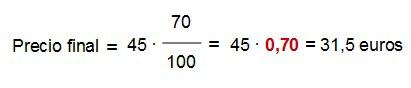
Ahora toca ver justo lo contrario:
Conocido el valor final y el porcentaje que ha disminuido el valor inicial, queremos saber dicho valor inicial.
Por ejemplo: Vas a las rebajas y en la etiqueta de una camiseta que te gusta marca que el precio rebajado un 40 % es de 14 euros. En la etiqueta pone que antes costaba 19,6 euros, pero como no te fías decides comprobarlo y calcular tú el precio que debería tener la camiseta inicialmente.
Lo primero es darse cuenta de que si ha habido un descuento o rebaja del 40 % sobre el precio inicial, el precio final de 14 euros se corresponde con el 60 % del precio inicial (100 % – 40 % = 60 %).
Podemos plantear entonces una regla de tres simple directa en la que aparezca el precio inicial como valor desconocido que corresponde al 100 %, y el precio final conocido de 14 euros que corresponde al 60 %:
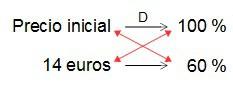
y aplicando la regla de tres…

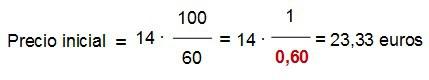
Si la rebaja es del 40 % y el precio final es de 14 euros, entonces el precio inicial (antes de la rebaja) debería haber sido de 23,33 euros, y no 19,6 euros como marca la etiqueta. Así es que…
¡Algo raro hay en todo esto!
Ahora después continuaremos investigando, pero antes fijémonos en que, análogamente a lo que ocurría en los aumentos porcentuales, para obtener el valor inicial conociendo el valor final y el porcentaje que ha disminuido, basta con dividir el valor final entre el correspondiente factor de porcentaje de la disminución.

En el caso que hemos visto de la camiseta rebajada el 40 %, dicho factor de porcentaje de disminución del valor inicial al 60 % es 0,60.
Si, por ejemplo, la rebaja o disminución hubiese sido de un 25 % dividiríamos el valor final entre 0,75 (factor de porcentaje correspondiente al 75 %) para obtener el valor inicial.
Veamos por último, como hicimos con los aumentos porcentuales, la tercera situación posible…
Una cantidad (un precio por ejemplo) ha disminuído de un valor inicial a un valor final y queremos saber en qué porcentaje lo ha hecho.
¡Y qué mejor que hacerlo con nuestra etiqueta sospechosa!
Según la etiqueta el precio inicial era de 19,6 euros, y el precio final (rebajado) es de 14 euros. Vamos a calcular el porcentaje que, con esos dos datos, se habría rebajado el precio de la camiseta.
Calculamos la diferencia entre el valor inicial y el valor final para saber en qué cantidad ha disminuído…
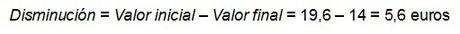
Nota: Si observáis, en este caso he restado al valor inicial el valor final (y no al final el inicial como hice en el caso del aumento porcentual). Simplemente lo he hecho para que salga un resultado positivo, ya que en una disminución el valor inicial es lógicamente mayor que el final. Lo hago así (se podría hacer al revés y que saliese negativo) porque personalmente me parece más natural dar la diferencia positiva e indicar que es una disminución que darla negativa. Pero habrá quien prefiera no hacerlo así.
Ahora vemos qué porcentaje representan esos 5,6 euros respecto del valor inicial.
Para ello planteamos la correspondiente regla de tres o, como vimos en su momento, dividimos diréctamente la parte (los 5,6 euros) entre el total (19,6 euros) y multiplicamos después por cien:
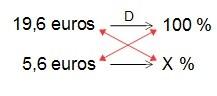
de donde…
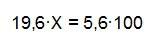
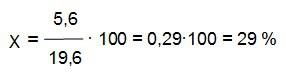
En realidad, si el precio inicial era el que marca la etiqueta, la rebaja es de un 29 % y no del 40 %.
Muy enfadados nos vamos al mostrador de la tienda y señalando al 40 % de nuestra etiqueta decimos:
¡Esto sólo está rebajado un veintinueve por ciento!
Tras un silencio y una mirada cómplice entre las dos personas que están atendiendo, una de ellas nos contesta:
¡Ay! Es que el 40 % es de los 14 euros, no de los 19,6 euros.
Pero a nosotros, que ya sabemos de esto y tenemos claro que los porcentajes de descuentos se aplican sobre el precio inicial y no sobre el final, no nos la van a “colar”.
Bueno…
¿Qué tal?
Ya sé que hemos hablado de bastantes cosas en poco tiempo y de hecho podría haber dividido todo esto que os he contado en varias entradas o “capítulos”, pero he preferido que estuviese todo en una.
Podría haber sido también mucho más directo y prácticamente poner una fórmula para cada caso, de manera que hubiesen sido unas pocas líneas. De hecho quizás haya bastantes personas que entraran buscando eso, pero ese no es mi estilo y ya son muchos los libros y los sitios donde se hace así.
A veces es bueno dedicarle a las cosas un tiempo, el justo (no se trata tampoco de malgastarlo), pero que nos permita entenderlas bien para después “correr” si queremos.
Y digo todo esto porque, en realidad, casi todo lo que hemos visto lo podemos resumir ahora (y no antes) en unas lineas:
Sé el total y quiero calcular la parte correspondiente a, por ejemplo, un 20 %… multiplico el total por 0,20.
Al revés… Lo que sé es la parte correspondiente a ese 20 % y quiero calcular el total… divido la parte por 0,20.
Conozco el total y la parte, y quiero saber cuál es el % de esa parte respecto del total… divido la parte entre el total y después multiplico por cien.
Un valor inicial varía, por ejemplo, un 10 % y quiero saber el valor final… multiplico dicho valor inicial por 1,10 si es un aumento (calculo el 110 %) o por 0,90 si es una disminución (calculo el 90 %).
Al revés… Lo que conozco es el valor final después de variar el valor inicial un 10 %, y quiero calcular dicho valor inicial… divido el valor final por 1,10 si es un aumento o por 0,90 si es una disminución.
Sé el valor inicial y el valor final, y quiero conocer el % que ha variado… hago la diferencia entre los dos (al mayor le resto el menor), lo divido entre el valor inicial y después lo multiplico por cien, e indico si es un aumento o una disminución.
Pero sinceramente, aprenderse esto sin entender lo demás no tiene sentido, porque no tendremos ni idea de qué estamos haciendo y menos aún sabremos utilizarlo cuando lo necesitemos de verdad. Estaremos calculando cosas pero, no nos engañemos, no sabremos calcularlas.
Si hasta ahora no sabíais calcular porcentajes o, aun sabiendo lo básico, no habíais visto tantas posibles situaciones, os recomiendo que lo leáis con detenimiento las veces que os hagan falta. Incluso podéis leer por partes la entrada, porque soy consciente que asimilar tanta información requiere un tiempo y no es instantáneo. Lo importante es que al final lo entendáis y podáis aplicarlo.
Pues ya hemos terminado.
Espero que os sea de utilidad, y cualquier duda o aclaración que necesitéis no dudéis en escribir un comentario.
¿Y la animación?
No me he olvidado, lo prometido es deuda.
En esta animación, aquello que dijimos al comienzo de la entrada de que el tanto por ciento de una cantidad se refería a la parte proporcional de cada cien unidades de dicha cantidad, se lleva al extremo interpretándolo literalmente y mostrando cómo sería nuestro planeta si sólo viviesen 100 personas en él.
Espero que os guste.
http://matematicascercanas.com/wp-content/uploads/2016/07/Si-100-personas-vivieran-en-la-Tierra.mp4Vídeo visto en Bright Side (http://brightside.me/)

