Problemas resueltos de Probabilidades

El departamento de investigación de mercados de Pepsico planea realizar una encuesta entre adolescentes sobre un refresco recién creado. A cada uno de ellos se le va a pedir que lo comparen con su refresco favorito.

• ¿En qué consiste el experimento? 

           Contrastar el refresco objeto de investigación contra el favorito de los adolescentes                              entrevistados.

• ¿Cúal es uno de los eventos posibles?

          Un evento posible es: "Preferir el nuevo refresco"
El número de veces que ocurrió un evento en el pasado se divide entre el número de veces que ocurre. ¿Cómo se llama este enfoque de la probabilidad?
      Se denomina probabilidad empírica.
La probabilidad de que la causa y la cura de todo tipo de cáncer se descubra antes del año 2020 es de 0.20. ¿Qué enfoque de la probabilidad ilustra este enunciado?
      Se denomina probabilidad subjetiva.
Berdine´s Chicken Factory posee varias tiendas en el área del Hilton Head, Carolina del Sur. Al entrevistar a los candidatos para el puesto de mesero, al propietario le gustaría incluir información referente a la propina que un mesero espera ganar por cuenta (o nota). Un estudio de 500 cuentas recientes indicó que el mesero ganaba las siguientes propinas por turno de 8 horas.

Propina Número

$0 a $ 20 200

$20 a $50 100

$50 a $100 75

$100 a $200 75

$200 o más 50

Total 500

• ¿Cuál es la probabilidad de que una propina sea de $200 o más?

      Sea x el valor de la propina, entonces:

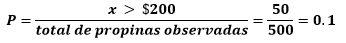
• ¿Las categorías $0 a $20, $20 a $50, etc., se consideran mutuamente excluyentes?

      Sólo bajo la premisa de que los valores son tomados en cuenta en un solo intervalo, puesto que el       límite superior de un intervalo y el límite inferior del siguiente intervalo son los mismos, entonces       se puede afirmar que los eventos definidos por dichas categorías constituyen eventos mutuamente       excluyentes.

• Si las probabilidades relacionadas con cada resultado se sumaran, ¿cuál sería el total?

      El total sería 1

• ¿Cuál es la probabilidad de que una propina sea de $50?

      Si definimos que el valor de $50 pertenece al intervalo $50 a $100, entonces:

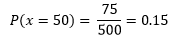
• ¿De que una propina sea inferior a $200?

      Sea x el valor de la propina, entonces:

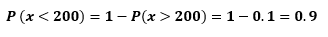
Ganar en todas las carreras "Triple Corona" se considera la mayor hazaña de un caballo de carreras de pedigrí. Después de un exitoso Derby de Kentucky, Big Brown es favorito 1 a 2 para ganar las apuestas de Preakness.

• Si Big Brown es favorito 1 a 2 para ganar las apuestas de Belmont también, ¿Cuál es la probabilidad de que gane la triple corona?

          Que Big Brown sea favorito para ganar las apuestas de Preakness significa que:

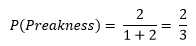
          Que Big Brown sea favorito para ganar las apuestas de Belmont significa que:

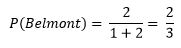
          Por tanto, la probabilidad de ganar la "Triple Corona" es:

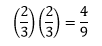
• ¿Cuáles tendrían que ser sus oportunidades para las apuestas de Preakness para que sea una "apuesta segura" para ganar la Triple Corona?

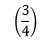
La primera carta de una baraja de 52 cartas es un rey. 

• Si lo regresa a la baraja, ¿cuál es la probabilidad de sacar un rey en la segunda selección?

          Sea x el evento de sacar un rey, entonces:

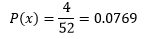
• Si no lo regresa a la baraja, ¿cuál es la probabilidad de sacar un rey en la segunda selección?

          Sea x el evento de sacar un rey, entonces:

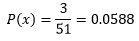
• ¿Cuál es la probabilidad de seleccionar un rey en la primera carta que se toma de la baraja y otro rey en la segunda (suponiendo que el primer rey no fue reemplazado)?

         Sea x el evento de sacar un rey en la primera carta y sea y el evento de sacar un rey en la                      segunda carta, entonces:

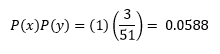
Armco, un fabricante de sistemas de semáforos, descubrió que, en las pruebas de vida acelerada, 95% de los sistemas recién desarrollados duraban 3 años antes de descomponerse al cambiar de señal.

• Si una ciudad comprara cuatro de estos sistemas, ¿cuál es la probabilidad de que los cuatro sistemas funcionen durante 3 años por lo menos?

         Sea x el evento de que un sistema dure 3 años, entonces:
P(x) = 0.95
         Dado que son 4 sistemas, entonces la probabilidad de que los cuatro sistemas funcionen                      adecuadamente durante al menos 3 años estará dada por:

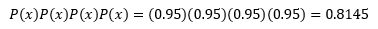
• ¿Qué regla de probabilidad se ejemplifica en este caso?

         Regla del producto para eventos independientes.

• Representando los cuatro sistemas con letras, escriba una ecuación para demostrar como llegó a la respuesta a.

          Dado los siguientes eventos independientes:
          A: El sistema A dura al menos 3 años.          B: El sistema B dura al menos 3 años.          C: El sistema C dura al menos 3 años.          D: El sistema D dura al menos 3 años.
          Entonces:

Observe el siguiente dibujo:

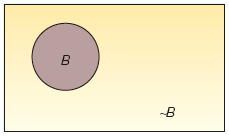
• ¿Qué nombre recibe el dibujo?

          Recibe el nombre de Diagrama de Venn

• ¿Qué regla de probabilidad se ilustra?

          Regla del complemento

• B representa el evento que se refiere a la selección de una familia que recibe prestaciones sociales. ¿A qué es igual P(B) + P(~B)?

          1
En un programa de empleados que realizan prácticas de gerencia en Claremont Enterprise, 80% de los empleados son mujeres y 20% hombres. 90% de las mujeres fueron a la universidad y 78% de los hombres fueron a la universidad.

• Al azar se elige un empleado que realiza prácticas de gerencia. ¿Cuál es la probabilidad de que la persona seleccionada sea una mujer que no asistió a la universidad?

          Sea x el evento de elegir una mujer. Sea y el evento de elegir a alguien que no fue a la                         universidad. Entonces: 

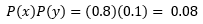
• ¿El género y la asistencia a la universidad son independientes?¿Porqué?

          No son eventos independientes dado que los datos indican que hay una relación entre el                       porcentaje de hombres (78%) y mujeres (90%) que fueron a la universidad.

• Construya un diagrama de árbol que muestre las probabilidades condicionales y probabilidades conjuntas.

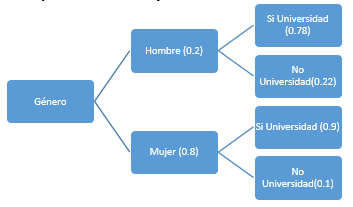
• Las probabilidades conjuntas suman 1.00 ¿Porqué?

          Las probabilides conjuntas deben sumar 1 dado que se enuncian todos los posibles resultados.


Suponga que la probabilidad de que cualquier vuelo de Nortwest Airlines llegue 15 minutos después de la hora programada es de 0.90. Seleccione cuatro vuelos de ayer para estudiarlos.

• ¿Cuál es la probabilidad de que los cuatro vuelos seleccionados lleguen 15 minutos de la hora programada?

          Sea x el evento de seleccionar un vuelo con retardo de 15 minutos. Entonces:

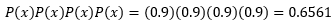
• ¿De que ninguno de los vuelos seleccionados llegue 15 minutos después de la hora programada?

          Sea x el evento de seleccionar un vuelo que llegue sin retardo. Entonces:

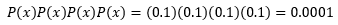
• ¿De que por lo menos uno de lols vuelos seleccionados no llegue 15 minutos después de la hora programada?

          Sea x el evento de seleccionar un vuelo que llegue sin retardo. Entonces  la probabilidad estará           dada por:

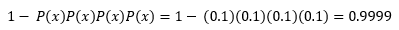
Estos ejercicios resueltos pertenecen al libro "Estadística aplicada a los negocios y la economía" - Décima Quinta Edición - Lind | Marchal | Wathen. Puede obtener un documento en formato PDF de los ejercicios aquí mostrados en la página de descargas.