¡Qué nadie se asuste con esto de los binomios conjugados, que os va a sonar y mucho!
En una entrada anterior os hablaba del cuadrado del binomio, una de esas identidades notables que aparecen inesperadamente en nuestra vida estando en clase de matemáticas:
(a + b)2 = a2 + b2 + 2ab
Y vimos su demostración gráfica…
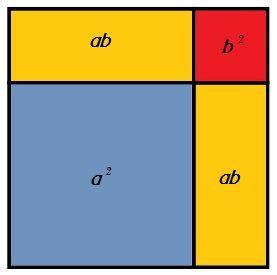
En esta ocasión vamos a ver otro “clásico” que acompaña en esa aparición estelar y repentina al cuadrado del binomio: el producto de binomios conjugados.
¿Binomios qué?
Espera, mejor así…
(a + b)(a – b) = a2 – b2
Aquello de suma por diferencia es igual a diferencia de cuadrados.
Demostrar esto es bastante sencillo, pues basta con “echar cuentas”…
(a + b)(a – b) = a2 – ab + ba – b2 = a2 – b2
(gracias a la propiedad conmutativa del producto, ab y ba son iguales y se anulan entre si)
Pero esta entrada no la he hecho para contaros esto, sino para ver su demostración gráfica, que considero es bastante más interesante.
¿Interesante por qué?
Pues por su sencillez. Y es que, desde mi punto de vista, cuanto más sencillas son las cosas, mejores y más elegantes son.
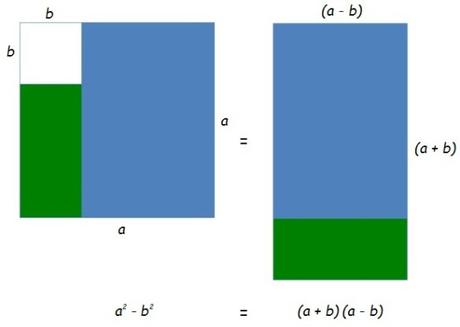
Dibujemos la parte de la derecha de la expresión, a2 – b2, es decir, lo de “diferencia de cuadrados”, que no es otra cosa que un cuadrado de lado a, de área a2, al que quitamos otro de lado b, de área b2…
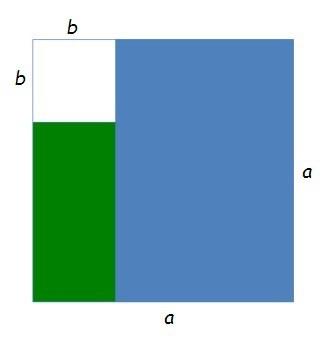
La parte coloreada (en verde y azul) de la figura anterior representa entonces a2 – b2.
Y ahora, simplemente moviendo el rectángulo verde, conservando por tanto el área coloreada, tenemos…
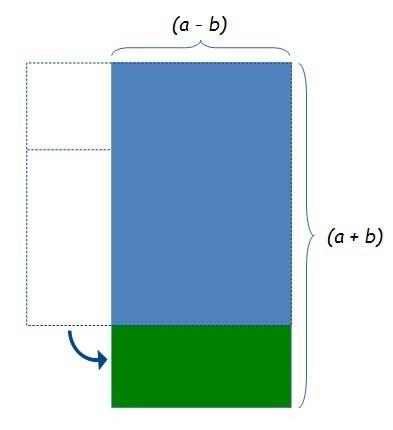
Un rectángulo cuyo área (a + b)(a – b) es igual al área de la figura anterior, a2 – b2.
¡Hemos demostrado lo que queríamos!
Y ya para terminar, lo ponemos todo junto, que se ve mejor…