Progresión aritmética… ¡Será por diferencias!

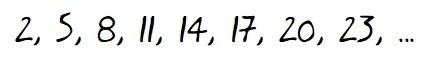
Esto que acabo de poner es un ejemplo de progresión aritmética.

¿Que qué es eso de una progresión aritmética?

Es una sucesión en la que cada término (excepto el primero) se obtiene sumando al anterior un número o cantidad fija que llamamos diferencia. Esa cantidad que sumamos puede ser positiva o negativa.

Que lo de antes es una sucesión parece claro (o al menos de números), porque son números dispuestos uno a continuación de otro, pero vamos a ver si se cumple eso de que cada término se obtiene sumando al anterior siempre el mismo número (la diferencia)…

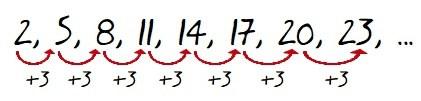
Pues sí, cada término lo obtenemos sumando al que va justo antes 3, y ocurre siempre. Luego efectivamente es una progresión aritmética y además de diferencia 3.

Antes de seguir contándote más cosas (esto es solo el comienzo) voy a hacer algo que nos gusta mucho en matemáticas y que es expresar todo esto “con letras”.

¡Ya estamos con las letras!

Créeme que nos va a ser útil, porque así las conclusiones que saquemos nos valdrán para cualquier caso de forma general, y no solo para uno en particular.

 Los términos de la progresión los vamos a identificar con una a con un subíndice que indica la posición del término en la progresión. Así a₁ será el primer término de la progresión, a₂ el segundo, a₃ el tercero… a₂₀ el término de la progresión que ocupa la posición 20…

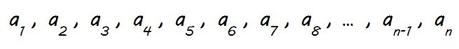
Si es una progresión aritmética hemos dicho que cada término (excepto el primero, a₁) se obtiene sumando al anterior la diferencia, que vamos a designar con la letra d. Es decir…

a₂ = a₁ + d

a₃ = a₂ + d

a₄ = a₃ + d

…

a_n = a_n-1 + d

 O, lo que es equivalente:

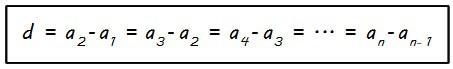
Y esto que acabamos de deducir es una de las formas (no es la única) que tenemos de calcular la diferencia en una progresión aritmética:

Cuando conocemos dos términos consecutivos de una progresión aritmética podemos calcular la diferencia de la progresión restando al término que va después el inmediato anterior.

Volviendo a la progresión aritmética con la que empezamos…

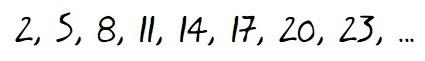
efectivamente se cumple que:

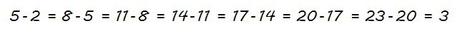
Bueno, ya tenemos claro que sumando a partir del primer término (a₁) sucesivamente la diferencia (d) se van obteniendo los términos de la progresión aritmética…

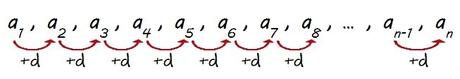
Pues sabiendo esto podemos, por ejemplo, calcular el quinto término (a₅) a partir del segundo (a₂) directamente sin tener que calcular previamente a₃ ni a₄, ya que al avanzar 3 posiciones (5 – 2 = 3) lo que hacemos es sumar tres veces la diferencia (d+d+d = 3d)…

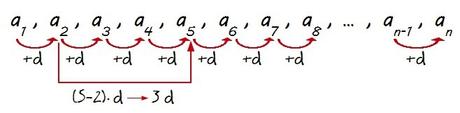
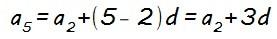
O, por ejemplo, calcular el octavo término (a₈) a partir del tercero (a₃), ya que como avanzamos 5 posiciones (8 – 3 = 5) sumamos cinco veces la diferencia (d+d+d+d+d = 5d)…

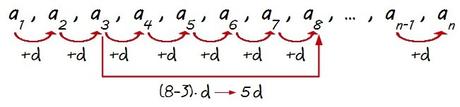
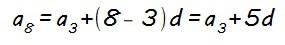
Y esto que acabamos de deducir es realmente útil a la hora de trabajar con progresiones aritméticas, porque nos permite calcular un término cualquiera de la progresión a partir de otro conociendo la diferencia (d), sin necesidad de que sean consecutivos.

Si llamamos a_p a un término genérico que ocupe la posición p y a_q a un término que ocupe la posición q, siendo p<q (el término a_p aparece antes en la progresión que el término a_q)…

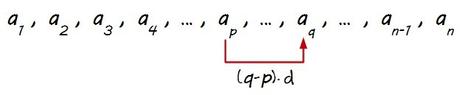
ambos términos se relacionan a través de la diferencia (d) de la forma:

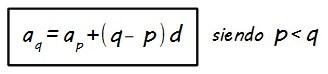
 Es lo mismo que hemos visto en los dos ejemplos anteriores pero generalizando.

Pero lo que es mejor aún es que esta expresión nos permite calcular la diferencia (d) conociendo dos términos cualesquiera de una progresión aritmética (a_p y a_q), ya que si sustituimos a_p y a_q por sus valores, y p y q por sus posiciones correspondientes, tenemos una ecuación en la que la única incógnita es d (la diferencia).

Por ejemplo, si a₂ = 5  y  a₇ = 20…

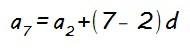
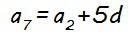
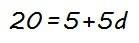
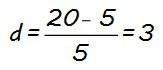
 Y todo esto que acabamos de ver lo podemos utilizar para definir la expresión del término general de una progresión aritmética (a_n), que nos permite calcular cualquier término de la misma:

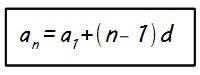
Si te fijas he utilizado como término de partida el primer término (a₁), aunque podría haber empleado cualquier otro, pero se suele hacer así ya que es el único término de la progresión aritmética que viene fijado de inicio y no se obtiene a partir de ninguno anterior.

Volviendo a nuestra progresión…

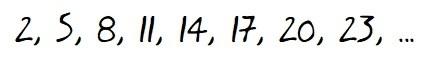
en la que hemos visto que d = 3   y  a₁ = 2, el término general de la misma será:

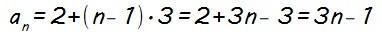
y, como he comentado antes, con esta expresión podemos calcular ahora el término de nuestra progresión aritmética que queramos, sustituyendo simplemente n por la posición que ocupa dicho término.

Por ejemplo:

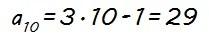
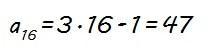
y así los que queramos.

Bien, ya sabemos obtener la diferencia de una progresión aritmética, calcular términos de la misma y obtener la expresión del término general.

Antes de explicarte algo más sobre las progresiones aritméticas…

… ¿Conoces la historia que se cuenta del matemático Gauss cuando tenía nueve años?

¿No la conoces?

En 1786, en una clase de Aritmética de tercero de primaria, un maestro rural llamado Büttner pidió a sus alumnos que hallaran la suma de los 100 primeros números (1+2+3+4+5+6+…+98+99+100). Un alumno de esa clase llamado Carl Friedrich Gauss, que entonces tenía 9 años, halló la respuesta correcta en muy poco tiempo, diciendo «Ligget se’» (“ya está”). Al acabar la hora se comprobaron las soluciones y se vio que la solución de Gauss era correcta, mientras que no lo eran muchas de las de sus compañeros.

La respuesta que Gauss dio fue: 5050. Si hacéis las 99 sumas que hay en la suma de los cien primeros números naturales llegaréis a esa solución, aunque tardando bastante más de lo que tardó aquel joven muchacho.

En el siguiente fragmento de la película alemana “Midiendo el mundo” (“Die Vermessung der Welt”) se recrea la escena de esa clase de Aritmética de la que os hablo:

https://matematicascercanas.com/wp-content/uploads/2014/05/Gauss-Midiendo-el-Mundo.mp4

Lo que Gauss observó fue que si sumaba el primer número con el último (1+100), el segundo con el penúltimo (2+99), el tercero con el antepenúltimo (3+98) y siguiendo así, podía realizar en total cincuenta sumas que daban como resultado siempre 101, por lo que concluyó que como 50 veces 101 era 5050, la suma de los cien primeros números naturales era entonces 5050.

Si os fijáis, lo que aquél maestro llamado Büttner pidió a sus alumnos no fue otra cosa que la suma de los 100 primeros términos de una progresión aritmética con a₁=1 y d=1.

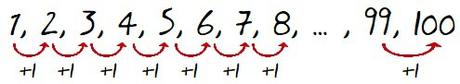
 Pues bien, utilizando esta idea, vamos a intentar deducir una expresión que nos permita calcular la suma de n términos de una progresión aritmética (S_n).

Tenemos nuestra progresión expresada de forma general…

Queremos calcular la suma de n términos de una progresión aritmética (S_n), que puedo expresar de dos formas diferentes:

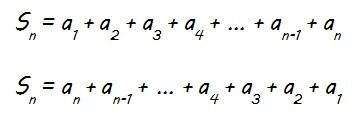
Sumando ambas expresiones tenemos:

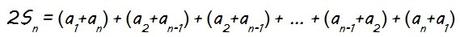
Si observamos…

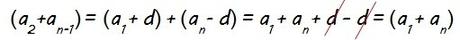
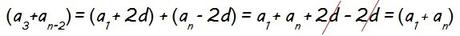
es decir, todos los sumandos que aparecen entre paréntesis en la expresión de antes equivalen a (a₁+a_n), por lo que…

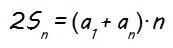
y, dividiendo ambos términos entre dos, obtenemos:

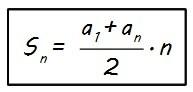
Expresión con la que podemos calcular la suma de n términos de una progresión aritmética (S_n) conociendo la diferencia d y el primer y último términos (a₁ y a_n).

¡Genial!

¡Ya sabemos hacer otra cosa más!

Con esta expresión, calcular la suma de los 100 primeros números naturales que se cuenta que hizo en aquella clase Gauss es muy rápido:

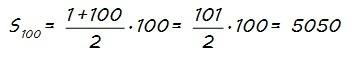
O. puestos ya, de los 10000 primeros…

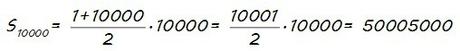
Bueno…

¿Qué tal?

Espero que hayas entendido bien todo esto que te he contado sobre las progresiones aritméticas. Es fundamental comprenderlo para saber utilizarlo correctamente y poder resolver cualquier tipo de ejercicio.

Piensa que son “herramientas” que tienes y que, como tales, debes saber cuál de ellas utilizar según lo que necesites en cada momento.

Puede parecer que son muchas cosas, pero en realidad no lo son. Te las resumo:

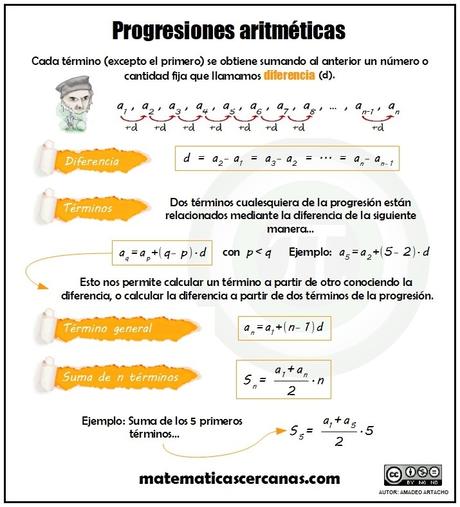
Por si te ha quedado alguna duda… ¿Quieres que veamos unos ejemplos?

---

EJEMPLO 1.

 En la siguiente progresión aritmética:

3, 18, 33, 48, …

Calcular el término general de la progresión (a_n) y la suma de los 10 primeros términos (S₁₀).

Lo primero que tenemos que hacer es calcular la diferencia (d) de la progresión, pues no nos la dan directamente, y de paso comprobamos que efectivamente es una progresión aritmética:

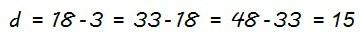
Nos piden calcular el término general (a_n) cuya expresión es:

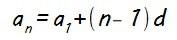
La diferencia ya la hemos calculado, d = 15, y el primer término (a₁) nos lo dan en el enunciado (es el primero que aparece en la progresión), a₁ = 3. Sustituyendo, tenemos que:

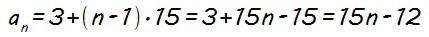
Esta es la expresión del término general de esta progresión aritmética. Con él, como ya comentamos, podemos calcular cualquier término de la misma.

Como comprobación vamos a calcular, por ejemplo, el tercer término (a₃):

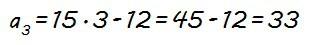
que efectivamente coincide con el tercer término de la progresión que nos dan.

Ahora vamos a calcular lo otro que nos piden: la suma de los 10 primeros términos (S₁₀).

La expresión de la suma de n términos (S_n) es…

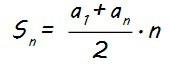
Sustituyendo n por 10, tenemos que la expresión de la suma de los 10 primeros términos es:

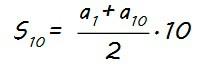
El valor de a₁ lo conocemos, a₁ = 3, pero necesitamos calcular a₁₀, y podemos hacerlo utilizando la expresión anterior que hemos obtenido del término general considerando n=10:

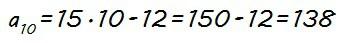
Sustituyendo ahora a₁ y a₁₀  por sus valores, la suma de los 10 primeros términos de la progresión aritmética que nos dan es:

---

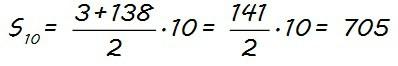
EJEMPLO 2.

Calcula el término general (a_n) y la suma de los 8 primeros términos (S₈) de una progresión aritmética de diferencia d = 4  y quinto término a₅ = 40.

En este caso la diferencia nos la dan como dato (d = 4), así que no tenemos que calcularla.

Nos piden calcular el término general (a_n) cuya expresión es:

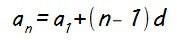
Para poder hacerlo, necesitamos calcular primero a₁.

Para ello basta con que lo relacionemos con el término que nos dan como dato (a₅) utilizando la expresión que vimos que relacionaba dos términos cualesquiera de la progresión:

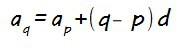
En nuestro caso concreto:

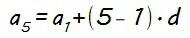
que, sustituyendo los valores conocidos de a₅ y d, queda:

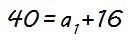
Y, despejando a₁ y operando…

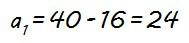
Si te fijas, lo que hemos hecho en definitiva es restar al quinto término cuatro veces la diferencia para ir cuatro pasos atrás en la progresión y llegar así al primer término.

Ahora ya sí podemos calcular la expresión del término general (a_n) que, con a₁ = 24  y d = 4, será:

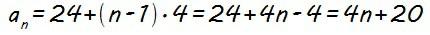
Para calcular ahora la suma de los 8 primeros términos (S₈) de la progresión aritmética, partimos de la expresión de S_n…

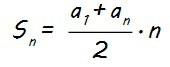
Sustituyendo n por 8, tenemos que la expresión de la suma de los 8 primeros términos es:

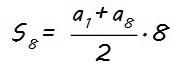
El valor de a₁ lo conocemos, a₁ = 24, pero necesitamos calcular a₈, y podemos hacerlo utilizando la expresión anterior que hemos obtenido del término general considerando n=8:

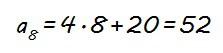
Sustituyendo ahora a₁ y a₈  por sus valores, la suma de los 8 primeros términos de la progresión aritmética que nos dan es:

---

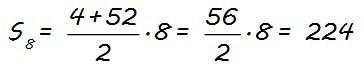
EJEMPLO 3.

Calcula el término general (a_n) y la suma de los 15 primeros términos (S₁₅) de una progresión aritmética de primer y tercer término a₁ = 14 y a₃ = 26.

Como nos ocurrió con el primer ejemplo, no nos dan como dato la diferencia (d), así que es lo primero que tenemos que calcular.

Como no conocemos dos términos consecutivos (los que tenemos son el primero y el tercero) no podemos restar a un término de la progresión su inmediato anterior para obtener la diferencia, pero sí podemos utilizar la expresión que relaciona dos términos cualesquiera de la progresión por medio de la diferencia (d):

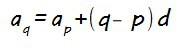
Lógicamente los dos términos que vamos a utilizar son los que nos dan como dato (de hecho no podemos hacer otra cosa) y en la ecuación que nos quede la única incógnita será la diferencia (d) que es lo que queremos calcular…

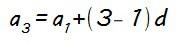
Si observas, lo que hemos hecho en definitiva es sumar al primer término dos veces la diferencia para ir dos pasos adelante en la progresión y llegar así al tercer término.

Sustituyendo a₁ y a₃ por sus valores…

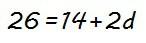
y despejando y operando, tenemos:

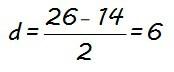
Pues ya tenemos la diferencia (d) y también el primer término (a₁) que nos lo dan como dato, así que podemos ya obtener la expresión del término general (a_n) de la progresión aritmética, que es lo primero que nos piden:

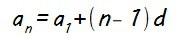
como a₁ = 14  y  d = 6, tenemos que:

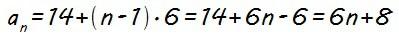
Bien, una cosa menos.

Vamos a calcular ahora la suma de los 15 primeros términos (S₁₅) de la progresión.

Partimos de la expresión de la suma de n términos (S_n):

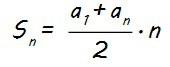
Sustituyendo n por 15, tenemos que la expresión de la suma de los 15 primeros términos es:

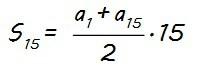
El valor de a₁ lo conocemos, a₁ = 14, pero necesitamos calcular a₁₅, y podemos hacerlo utilizando la expresión anterior que hemos obtenido del término general considerando n=15:

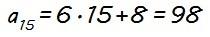
Sustituyendo ahora a₁ y a₁₅  por sus valores, la suma de los 15 primeros términos de la progresión aritmética que nos dan es:

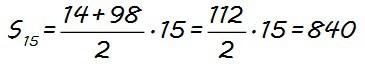
Espero que con estos tres ejemplos que hemos hecho te haya quedado todo más claro.

---

Suscríbete al blog por correo electrónico

Suscríbete de forma totalmente gratuita al blog y sé el primero en enterarte de las novedades.

Únete a otros 1.927 suscriptores

Dirección de correo electrónico